Midterm 02
Practice problems for topics on Midterm 02.
Tags in this problem set:
Problem #014
Tags: kernel ridge regression
Let \(\nvec{x}{1} = (1, 2, 0)^T\), \(\nvec{x}{2} = (-1, -1, -1)^T\), \(\nvec{x}{3} = (2, 2, 0)^T\), \(\nvec{x}{4} = (0, 2, 0)\).
Suppose a prediction function \(H(\vec x)\) is learned using kernel ridge regression on the above data set using the kernel \(\kappa(\vec x, \vec x') = (1 + \vec x \cdot\vec x')^2\) and regularization parameter \(\lambda = 3\). Suppose that \(\vec\alpha = (1, 0, -1, 2)^T\) is the solution of the dual problem.
Let \(\vec x = (0, 1, 0)^T\) be a new point. What is \(H(\vec x)\)?
Solution
18
Problem #015
Tags: regularization
Let \(R(\vec w)\) be the unregularized empirical risk with respect to the square loss (that is, the mean squared error) on a data set.
The image below shows the contours of \(R(\vec w)\). The dashed lines show places where \(\|\vec w\|_2\) is 2, 4, 6, etc.
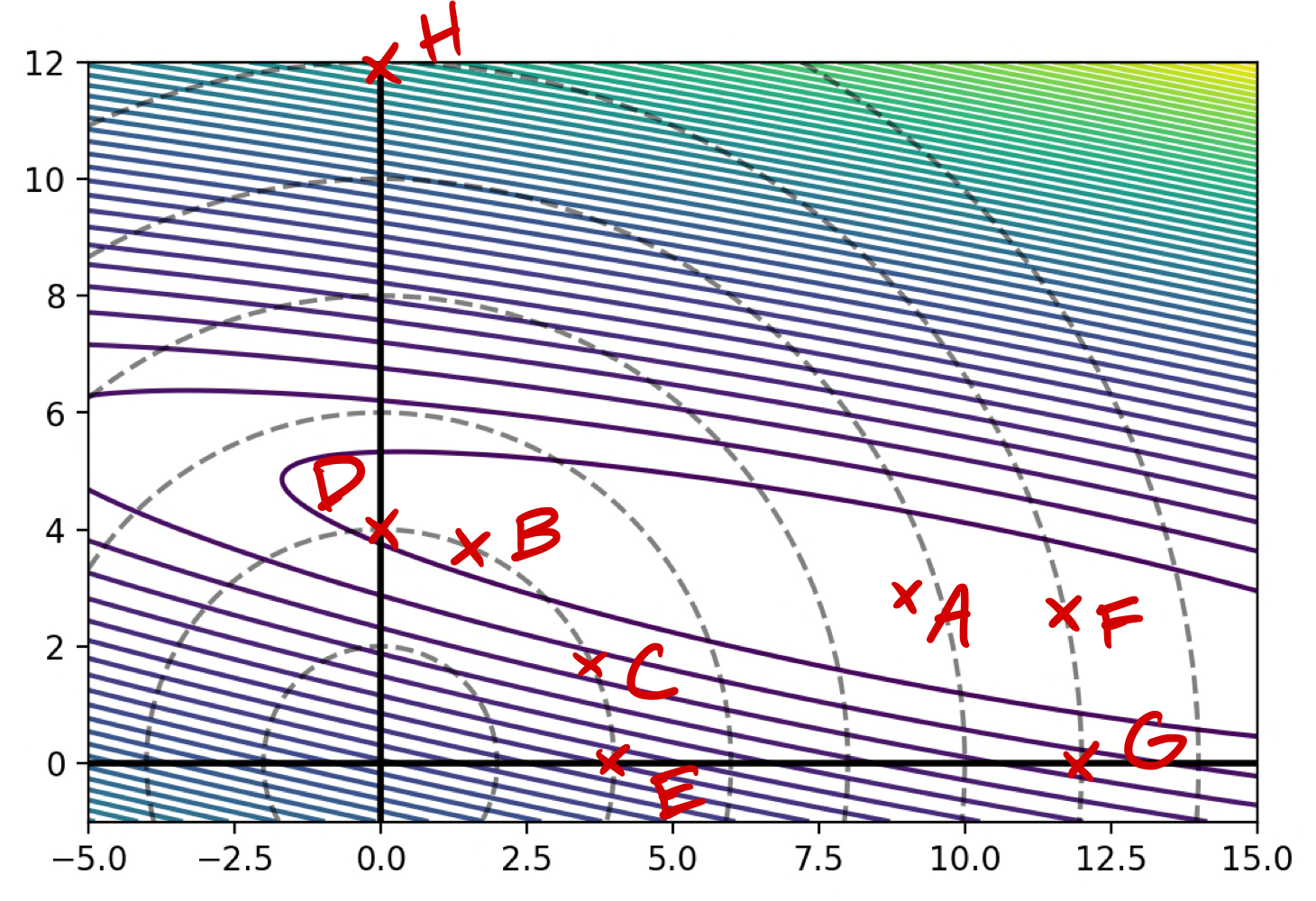
Part 1)
Assuming that one of the points below is the minimizer of the unregularized risk, \(R(\vec w)\), which could it possibly be?
Solution
A
Part 2)
Let the regularized risk \(\tilde R(\vec w) = R(\vec w) + \lambda\|\vec w \|_2^2\), where \(\lambda > 0\).
Assuming that one of the points below is the minimizer of the regularized risk, \(\tilde R(\vec w)\), which could it possibly be?
Solution
B
Problem #016
Tags: kernel ridge regression
Let \(\{\nvec{x}{i}, y_i\}\) be a data set of \(n\) points, with each \(\nvec{x}{i}\in\mathbb R^d\). Recall that the solution to the kernel ridge regression problem is \(\vec\alpha = (K + n \lambda I)^{-1}\vec y\), where \(K\) is the kernel matrix, \(I\) is the identity matrix, \(\lambda > 0\) is a regularization parameter, and \(\vec y = (y_1, \ldots, y_n)^T\).
Suppose kernel ridge regression is performed with a kernel \(\kappa\) that is a kernel for a feature map \(\vec\phi : \mathbb R^d \to\mathbb R^k\).
What is the size of the kernel matrix, \(K\)?
Solution
The kernel matrix is of size \(n \times n\).
Problem #030
Tags: kernel ridge regression
Consider the data set: \(\nvec{x}{1} = (1, 0, 2)^T\)\(\nvec{x}{2} = (-1, 0, -1)^T\)\(\nvec{x}{3} = (1, 2, 1)^T\)\(\nvec{x}{4} = (1, 1, 0)^T\) Suppose a prediction function \(H(\vec x)\) is learned using kernel ridge regression on the above data set using the kernel \(\kappa(\vec x, \vec x') = (1 + \vec x \cdot\vec x')^2\) and regularization parameter \(\lambda = 3\). Suppose that \(\vec\alpha = (-1, -2, 0, 2)^T\) is the solution of the dual problem.
Part 1)
What is the (2,3) entry of the kernel matrix?
\(K_{23} = \)
Part 2)
Let \(\vec x = (1, 1, 0)^T\) be a new point. What is \(H(\vec x)\)?
Problem #031
Tags: regularization
Let \(R(\vec w)\) be an unregularized empirical risk function with respect to some data set.
The image below shows the contours of \(R(\vec w)\). The dashed lines show places where \(\|\vec w\|_2\) is 1, 2, 3, etc.
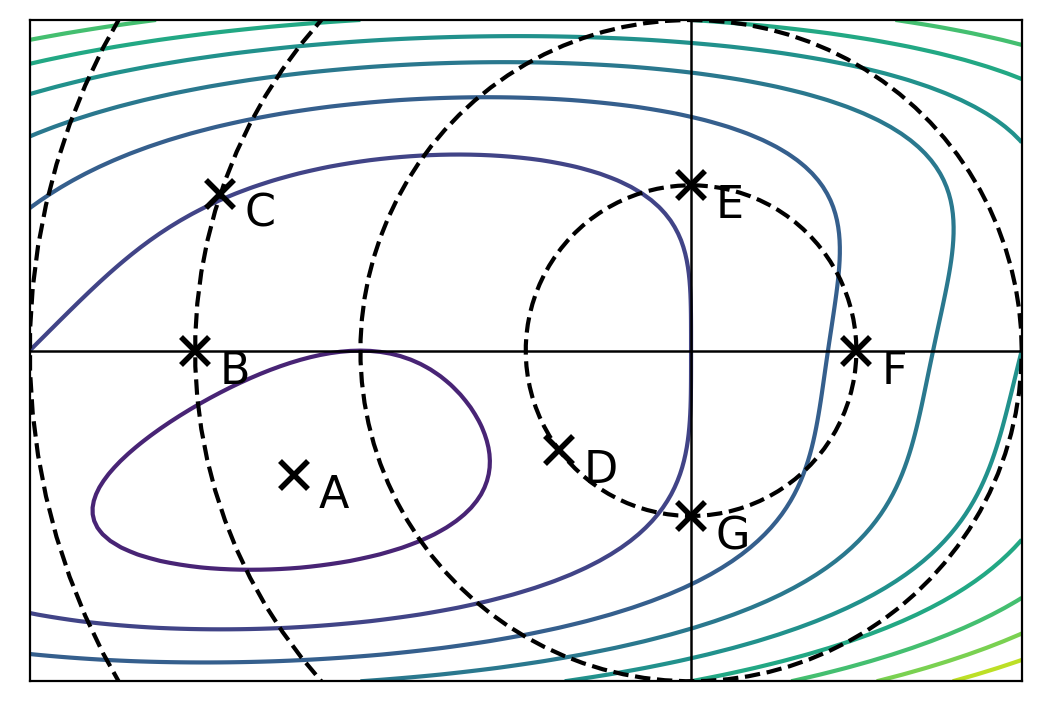
Part 1)
Assuming that one of the points below is the minimizer of the unregularized risk, \(R(\vec w)\), which could it possibly be?
Solution
A minimizer of the unregularized risk could be point A.
Part 2)
Let the regularized risk \(\tilde R(\vec w) = R(\vec w) + \lambda\|\vec w \|_2^2\), where \(\lambda > 0\).
Assuming that one of the points below is the minimizer of the regularized risk, \(\tilde R(\vec w)\), which could it possibly be?
Solution
A minimizer of the regularized risk could be point D.
Problem #032
Tags: bayes error, bayes classifier
Shown below are two conditional densities, \(p_1(x \,|\, Y = 1)\) and \(p_0(x \given Y = 0)\), describing the distribution of a continuous random variable \(X\) for two classes: \(Y = 0\)(the solid line) and \(Y = 1\)(the dashed line). You may assume that both densities are piecewise constant.

Part 1)
Suppose \(\pr(Y = 1) = 0.5\) and \(\pr(Y = 0) = 0.5\). What is the prediction of the Bayes classifier at \(x = 1.5\)?
Solution
Class 0
Part 2)
Suppose \(\pr(Y = 1) = 0.5\) and \(\pr(Y = 0) = 0.5\). What is the Bayes error with respect to this distribution?
Part 3)
Now suppose \(\pr(Y = 1) = 0.7\) and \(\pr(Y = 0) = 0.3\). What is the prediction of the Bayes classifier at \(x = 1.5\)?
Solution
Class 1
Part 4)
Now suppose \(\pr(Y = 1) = 0.7\) and \(\pr(Y = 0) = 0.3\). What is the Bayes error with respect to this distribution?
Problem #033
Tags: bayes classifier
Suppose the Bayes classifier achieves an error rate of 15\% on a particular data distribution. True or False: It is impossible for any classifier trained on data drawn from this distribution to achieve better than 85\% accuracy on a finite test set that is drawn from this distribution.
Solution
False.
Problem #034
Tags: histogram estimators
Consider the data set of ten points shown below:

Suppose this data is used to build a histogram density estimator, \(f\), with bins: \([0,2), [2, 6), [6, 10)\). Note that the bins are not evenly sized.
Part 1)
What is \(f(1.5)\)?
Part 2)
What is \(f(7)\)?
Problem #035
Tags: histogram estimators
Consider this data set of points \(x\) from two classes \(Y = 1\) and \(Y = 0\).

Suppose a histogram estimator with bins \([0,1)\), \([1, 2)\), \([2, 3)\) is used to estimate the densities \(p_1(x \given Y = 1)\) and \(p_0(x \given Y = 0)\), and these estimates are used in the Bayes classifier to make a prediction.
What will be the predicted class of a new point, \(x = 2.2\)?
Solution
Class 0.
Problem #036
Tags: density estimation, histogram estimators
Suppose a density estimate \(f : \mathbb R^3 \to\mathbb R^1\) is made using histogram estimators with bins having a length of 2 units, a width of 3 units, and a height of 1 unit.
What is the largest value that \(f(\vec x)\) can possibly have?
Problem #037
Tags: maximum likelihood
Suppose a discrete random variable \(X\) takes on values of either 0 or 1 and has the distribution:
where \(\theta\in[0, 1]\) is a parameter.
Given a data set \(x_1, \ldots, x_n\), what is the maximum likelihood estimate for the parameter \(\theta\)? Show your work.
Solution
The maximum likelihood estimate for \(\theta\) is the mean of all data points: \(\theta = \frac{1}{n}\sum_{i=1}^{n} x_i\) We can derive it as follows. First, set up the likelihood function
Then, to make our lives easier, we can find the log-likelihood before differentiating:
Problem #038
Tags: covariance
Consider a data set of \(n\) points in \(\mathbb R^d\), \(\nvec{x}{1}, \ldots, \nvec{x}{n}\). Suppose the data are standardized, creating a set of new points \(\nvec{z}{1}, \ldots, \nvec{z}{n}\). That is, if the new points are stacked into an \(n \times d\) matrix, \(Z\), the mean and variance of each column of \(Z\) would be zero and one, respectively.
True or False: the covariance matrix of the standardized data must be the \(d\times d\) identity matrix; that is, the \(d \times d\) matrix with ones along the diagonal and zeros off the diagonal.
Solution
False.
Problem #039
Tags: density estimation, maximum likelihood
Suppose data points \(\nvec{x}{1}, \ldots, \nvec{x}{n}\) are drawn from an arbitrary, unknown distribution with density \(f\).
True or False: it is guaranteed that, given enough data (that is, \(n\) large enough), a Gaussian fit to the data using the method of maximum likelihood will approximate the true underlying density \(f\) arbitrarily closely.
Solution
False.
Problem #040
Tags: Gaussians, maximum likelihood
Suppose a Gaussian with a diagonal covariance matrix is fit to 200 points in \(\mathbb R^4\) using the maximum likelihood estimators. How many parameters are estimated? Count each entry of \(\mu\) and the covariance matrix that must be estimated as its own parameter.
Problem #041
Tags: covariance
Suppose a data set consists of the following three measurements for each Saturday last year: \(X_1\): The day's high temperature \(X_2\): The number of people at Pacific Beach on that day \(X_3\): The number of people wearing coats on that day
Suppose the covariance between these features is calculated and placed into a \(3 \times 3\) sample covariance matrix, \(C\). Which of the below options most likely shows the sign of each entry of the sample covariance matrix?
Solution
The second option.
Problem #042
Tags: covariance
Suppose we have two data sets, \(\mathcal{D}_1\) and \(\mathcal{D}_2\), each containing \(n/2\) points in \(\mathbb R^d\). Let \(\nvec{\mu}{1}\) and \(C^{(1)}\) be the mean and sample covariance matrix of \(\mathcal{D}_1\), and let \(\nvec{\mu}{2}\) and \(C^{(2)}\) be the mean and sample covariance matrix of \(\mathcal{D}_2\).
Suppose the two data sets are combined into a single data set \(\mathcal D\) containing \(n\) points.
Part 1)
True or False: the mean of the combined data \(\mathcal{D}\) is equal to \(\displaystyle\frac{\nvec{\mu}{1} + \nvec{\mu}{2}}{2}\).
Solution
True.
Part 2)
True or False: the sample covariance matrix of the combined data \(\mathcal{D}\) is equal to \(\displaystyle\frac{C^{(1)} + C^{(2)}}{2}\).
Solution
False
Problem #043
Tags: covariance
Suppose a random vector \(\vec X = (X_1, X_2)\) has a multivariate Gaussian distribution. Suppose it is known that known that \(X_1\) and \(X_2\) are independent.
Let \(C\) be the Gaussian distribution's covariance matrix.
Part 1)
True or False: \(C\) must be diagonal.
Solution
True.
Part 2)
True or False: each entry of \(C\) must the same.
Solution
False.
Problem #044
Tags: naive bayes
Consider the below data set which collects information on 10 pets:
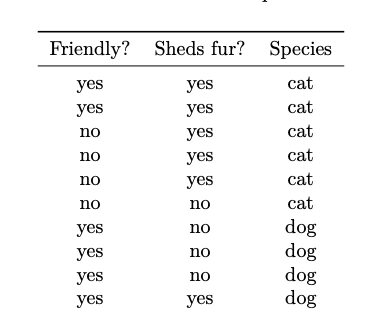
Suppose a new pet is friendly and sheds fur. What does a Na\"ive Bayes classifier predict for its species?
Solution
Cat.
Problem #045
Tags: naive bayes
Suppose a data set of 100 points in 10 dimensions is used in a binary classification task; that is, each point is labeled as either a 1 or a 0.
If Gaussian Naive Bayes is trained on this data, how many univariate Gaussians will be fit?
Problem #046
Tags: conditional independence
Recall that a deck of 52 cards contains:
Hearts: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A
Diamonds: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A
Clubs: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A
Spades: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A
Also recall that Hearts and Diamonds are red, while Clubs and Spades are black.
Part 1)
Suppose a single card is drawn at random.
Let \(A\) be the event that the card is a heart. Let \(B\) be the event that the card is a 5.
Are \(A\) and \(B\) independent events?
Solution
Yes, they are independent.
Part 2)
Suppose two cards are drawn at random (without replacing them into the deck).
Let \(A\) be the event that the second card is a heart. Let \(B\) be the event that the first card is red.
Are \(A\) and \(B\) independent events?
Solution
No, they are not.
Part 3)
Suppose two cards are drawn at random (without replacing them into the deck).
Let \(A\) be the event that the second card is a heart. Let \(B\) be the event that the second card is a diamond. Let \(C\) be the event that the first card is face card.
Are \(A\) and \(B\) conditionally independent given \(C\)?
Solution
No, they are not.
Problem #047
Tags: bayes error, bayes classifier
Part 1)
Suppose a particular probability distribution has the property that, whenever data are sampled from the distribution, the sampled data are guaranteed to be linearly separable. True or False: the Bayes error with respect to this distribution is 0\%.
Solution
True.
Part 2)
Now consider a different probability distribution. Suppose the Bayes classifier achieves an error rate of 0\% on this distribution. True or False: given a finite data set sampled from this distribution, the data must be linearly separable.
Solution
False.
Problem #048
Tags: histogram estimators
Consider this data set of points \(x\) from two classes \(Y = 1\) and \(Y = 0\).

Suppose a histogram estimator with bins \([0,2)\), \([2, 4)\), \([4, 6)\) is used to estimate the densities \(p_1(x \given Y = 1)\) and \(p_0(x \given Y = 0)\).
What will be the predicted class-conditional density for class 0 at a new point, \(x = 2.2\)? That is, what is the estimated \(p_0(2.2 \given Y = 0)\)?
Solution
1/6.
When estimating the conditional density, we look only at the six points in class zero. Two of these fall into the bin, and the bin width is 2, so the estimated density is:
Problem #049
Tags: histogram estimators
Suppose \(\mathcal D\) is a data set of 100 points. Suppose a density estimate \(f : \mathbb R^3 \to\mathbb R^1\) is constructed from \(\mathcal D\) using histogram estimators with bins having a length of 2 units, a width of 2 units, and a height of 2 units.
The density estimate within a particular bin of the histogram is 0.1. How many data points from \(\mathcal D\) fall within that histogram bin?
Problem #050
Tags: Gaussians
Suppose data points \(x_1, \ldots, x_n\) are independently drawn from a univariate Gaussian distribution with unknown parameters \(\mu\) and \(\sigma\).
True or False: it is guaranteed that, given enough data (that is, \(n\) large enough), a univariate Gaussian fit to the data using the method of maximum likelihood will approximate the true underlying density arbitrarily closely.
Solution
True.
Problem #051
Tags: maximum likelihood
Suppose a continuous random variable \(X\) has the density:
where \(\theta\in(0, \infty)\) is a parameter, and where \(x > 0\).
Given a data set \(x_1, \ldots, x_n\), what is the maximum likelihood estimate for the parameter \(\theta\)? Show your work.
Problem #052
Tags: covariance
Let \(\mathcal D\) be a set of data points in \(\mathbb R^d\), and let \(C\) be the sample covariance matrix of \(\mathcal D\). Suppose each point in the data set is shifted in the same direction and by the same amount. That is, suppose there is a vector \(\vec\delta\) such that if \(\nvec{x}{i}\in\mathcal D\), then \(\nvec{x}{i} + \vec\delta\) is in the new data set.
True or False: the sample covariance matrix of the new data set is equal to \(C\)(the sample covariance matrix of the original data set).
Solution
True.
Problem #053
Tags: Gaussians, maximum likelihood
Suppose a Gaussian with a diagonal covariance matrix is fit to 200 points in \(\mathbb R^4\) using the maximum likelihood estimators. How many parameters are estimated? Count each entry of \(\vec\mu\) and the covariance matrix that must be estimated as its own parameter (the off-diagonal elements of the covariance are zero, and shouldn't be included in your count).
Problem #054
Tags: Gaussians
Let \(f_1\) be a univariate Gaussian density with parameters \(\mu\) and \(\sigma_1\). And let \(f_2\) be a univariate Gaussian density with parameters \(\mu\) and \(\sigma_2 \neq\sigma_1\). That is, \(f_2\) is centered at the same place as \(f_1\), but with a different variance.
Consider the density \(f(x) = \frac{1}{2}(f_1(x) + f_2(x))\); the factor of \(1/2\) is a normalization factor which ensures that \(f\) integrates to one.
True or False: \(f\) must also be a Gaussian density.
Solution
False. The sum of two Gaussian densities is not necessarily a Gaussian density, even if the two Gaussians have the same mean.
If you try adding two Gaussian densities with different variances, you will get:
For this to be a Gaussian, we'd need to be able to write it in the form:
but this is not possible when \(\sigma_1 \neq\sigma_2\).
Problem #055
Tags: covariance
Consider the data set \(\mathcal D\) shown below.
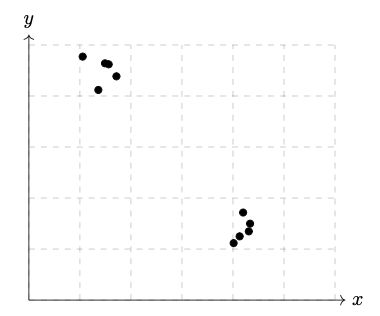
What will be the sign of the \((1,2)\) entry of the data's sample covariance matrix?
Solution
The sign will be negative.
Problem #056
Tags: linear and quadratic discriminant analysis
Suppose a data set of points in \(\mathbb R^2\) consists of points from two classes: Class 1 and Class 0. The mean of the points in Class 1 is \((3,0)^T\), and the mean of points in Class 0 is \((7,0)^T\). Suppose Linear Discriminant Analysis is performed using the same covariance matrix \(C = \sigma^2 I\) for both classes, where \(\sigma\) is some constant.
Suppose there were 50 points in Class 1 and 100 points in Class 0.
Consider a new point, \((5, 0)^T\), exactly halfway between the class means. What will LDA predict its label to be?
Solution
Class 0.
Problem #057
Tags: naive bayes
Consider the below data set which collects information on the weather on 10 days:

Suppose a new day is not sunny but is warm. What does a Na\"ive Bayes classifier predict for whether it rained?
Solution
Yes, it rained.
Problem #058
Tags: conditional independence
Suppose that a deck of cards has some cards missing. Namely, both the Ace of Spades and Ace of Clubs are missing, leaving 50 cards remaining.
Hearts: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A
Diamonds: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A
Clubs: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K
Spades: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K
Also recall that Hearts and Diamonds are red, while Clubs and Spades are black.
Part 1)
Suppose a single card is drawn at random.
Let \(A\) be the event that the card is a heart. Let \(B\) be the event that the card is an Ace.
Are \(A\) and \(B\) independent events?
Solution
No, they are not.
Part 2)
Suppose a single card is drawn at random.
Let \(A\) be the event that the card is a red. Let \(B\) be the event that the card is a heart. Let \(C\) be the event that the card is an ace.
Are \(A\) and \(B\) conditionally independent given \(C\)?
Solution
Yes, they are.
Part 3)
Suppose a single card is drawn at random.
Let \(A\) be the event that the card is a King. Let \(B\) be the event that the card is red. Let \(C\) be the event that the card is not a numbered card (that is, it is a J, Q, K, or A).
Are \(A\) and \(B\) conditionally independent given \(C\)?
Solution
No, they are not conditionally independent.
Problem #070
Tags: regularization
Recall that in ridge regression, we solve the following optimization problem:
where \(\lambda > 0\) is a hyperparameter controlling the strength of regularization.
Suppose you solve the ridge regression problem with \(\lambda = 2\), and the resulting solution is the weight vector \(\vec w_\text{old}\). You then solve the ridge regression problem with \(\lambda = 4\) and find a weight vector \(\vec w_\text{new}\).
True or False: each component of the new solution, \(\vec w_\text{new}\), must be less than or equal to the corresponding component of the old solution, \(\vec w_\text{old}\).
Solution
False.
While it is true that \(\|\vec w_\text{new}\|\leq\|\vec w_\text{old}\|\), this does not imply that each component of \(\vec w_\text{new}\) is less than or equal to the corresponding component of \(\vec w_\text{old}\).
The picture to have in mind is that of the contour lines of the mean squared error (which are ovals), along with the circles representing where \(\|\vec w\| = c\) for some constant \(c\). The question asked us to consider going from \(\lambda = 2\) to \(\lambda = 4\), but to gain an intuition we can think of going from no regularization (\(\lambda = 0\)) to some regularization (\(\lambda > 0\)); this won't affect the outcome, but will make the story easier to tell.
Consider the situation shown below:

When we had no regularization, the solution was \(\vec w_\text{old}\), as marked. Suppose we add regularization, and we're told that the regularization is such that when we solve the ridge regression problem, the norm of \(\vec w_\text{new}\) will be equal to \(c\), and that the radius of the circle we've drawn is \(c\). Then the solution \(\vec w_\text{new}\) will be the point marked, since that is the point on the circle that is on the lowest contour.
Notice that the point \(\vec w_\text{new}\) is closer to the origin, and it's first component is much smaller than the first component of \(\vec w_\text{old}\). However, the second component of \(\vec w_\text{new}\) is actually larger than the second component of \(\vec w_\text{old}\).
Problem #075
Tags: regularization
The ``inifinity norm'' of a vector \(\vec w \in\mathbb R^d\), written \(\|\vec w\|_\infty\), is defined as:
That is, it is the maximum absolute value of any entry of \(\vec w\).
Let \(R(\vec w)\) be an unregularized risk function on a data set. The solid curves in the plot below are the contours of \(R(\vec w)\). The dashed lines show where \(\|\vec w\|_\infty\) is equal to 1, 2, 3, and so on.
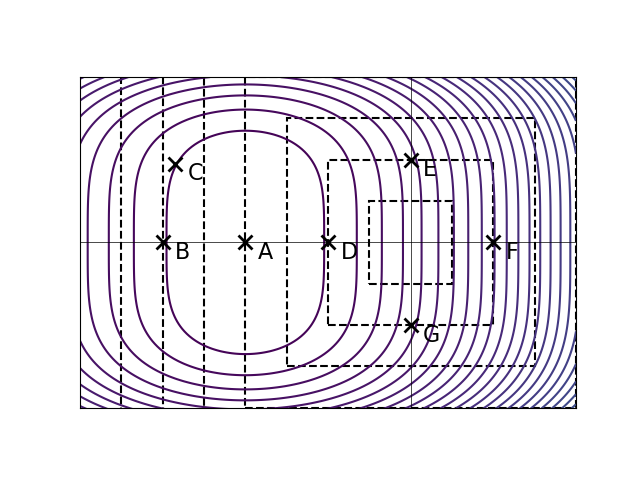
Let \(\tilde R(\vec w) = R(\vec w) + \lambda\|\vec w\|_\infty^2\), with \(\lambda > 0\). The point marked \(A\) is the minimizer of the unregularized risk. Suppose that it is known that one of the other points is the minimizer of the regularized risk, \(\tilde R(\vec w)\), for some unknown \(\lambda > 0\). Which point is it?
Solution
D.
Problem #086
Tags: regularization
Recall that in ridge regression, we solve the following optimization problem:
where \(\lambda > 0\) is a hyperparameter controlling the strength of regularization.
Suppose you solve the ridge regression problem with \(\lambda = 2\), and the resulting solution has a mean squared error of \(10\).
Now suppose you increase the regularization strength to \(\lambda = 4\) and solve the ridge regression problem again. True or False: it is possible that the mean squared error of the new solution is less than \(10\).
By ``mean squared error,'' we mean \(\frac1n \sum_{i=1}^n (y_i - \vec w \cdot\operatorname{Aug}(\nvec{x}{i}))^2\)
Solution
False.
Problem #091
Tags: regularization
The ``\(p = \frac12\)'' norm of a vector \(\vec w \in\mathbb R^d\), written \(\|\vec w\|_{\frac12}\), is defined as:
Let \(R(\vec w)\) be an unregularized risk function on a data set. The solid curves in the plot below are the contours of \(R(\vec w)\). The dashed lines show where \(\|\vec w\|_{\frac12}\) is equal to 1, 2, 3, and so on.
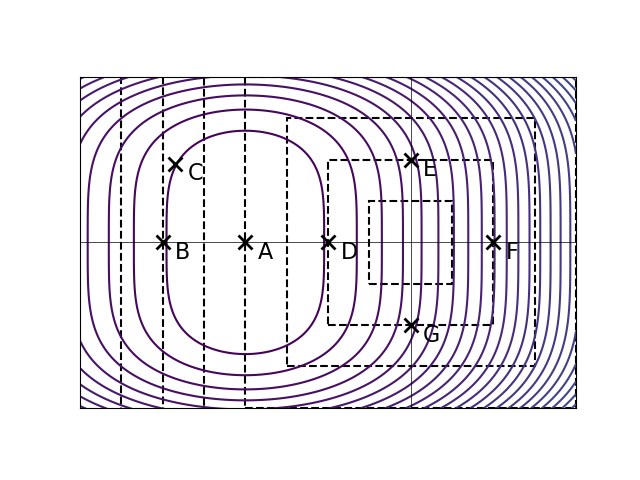
Let \(\tilde R(\vec w) = R(\vec w) + \lambda\|\vec w\|_{\frac12}\), with \(\lambda > 0\). The point marked \(A\) is the minimizer of the unregularized risk. Suppose it is known that one of the other points is the minimizer of the regularized risk, \(\tilde R(\vec w)\), for some unknown \(\lambda > 0\). Which point is it?
Solution
D.
Problem #092
Tags: kernel ridge regression
Suppose Gaussian kernel ridge regression is used to train a model on the following data set of \((x_i, y_i)\) pairs, using a kernel width parameter of \(\gamma = 1\) and a regularization parameter of \(\lambda = 0\):
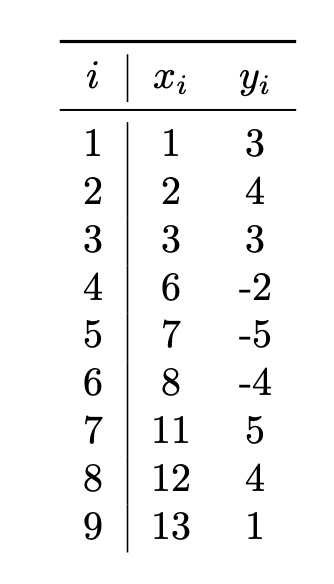
Let \(\vec\alpha\) be the solution to the dual problem. What will be the sign of \(\alpha_5\)?
Solution
Negative. Video explanation: https://youtu.be/K_1cxeQAkdk
Problem #093
Tags: bayes error, bayes classifier
Shown below are two conditional densities, \(p_1(x \,|\, Y = 1)\) and \(p_0(x \given Y = 0)\), describing the distribution of a continuous random variable \(X\) for two classes: \(Y = 0\)(the solid line) and \(Y = 1\)(the dashed line). You may assume that both densities are piecewise constant.

Part 1)
What is \(\pr(1 \leq X \leq 3 \given Y = 0)\)?
Part 2)
Suppose \(\pr(Y = 1) = \pr(Y = 0) = 0.5\). What is the prediction of the Bayes classifier at \(x = 2.5\)?
Solution
Class 0.
Part 3)
Suppose again that \(\pr(Y = 1) = \pr(Y = 0) = 0.5\). What is the Bayes error with respect to this distribution?
Part 4)
Now suppose \(\pr(Y = 1) = 0.7\) and \(\pr(Y = 0) = 0.3\). What is the prediction of the Bayes classifier at \(x = 2.5\)?
Solution
Class 1.
Part 5)
Suppose again that \(\pr(Y = 1) = 0.7\) and \(\pr(Y = 0) = 0.3\). What is the Bayes error with respect to this distribution?
Solution
Video explanation: https://youtu.be/mczKmVUJauI
Problem #094
Tags: histogram estimators
In this problem, consider the following labeled data set of 15 points, 5 from Class 1 and 10 from Class 0.

Suppose the class conditional densities are estimated using a histogram estimator with bins: \([0, 3), [3, 5), [5, 6),\) and \([6, 10)\). Note that the bins are not all the same width!
In all of the parts below, you may write your answer either as a decimal or as a fraction.
Part 1)
What is the estimate of the Class 0 density at \(x = 3.5\)? That is, what is the estimate for \(p(3.5 \given Y = 0)\)?
Part 2)
Using the same histogram estimator, what is the estimate of \(\pr(Y = 1 \given x = 3.5)\)?
Solution
Video explanation: https://youtu.be/0WFYpsDapC8
Problem #095
Tags: kernel ridge regression
Suppose a prediction function \(H(\vec x)\) is trained using kernel ridge regression on the data below using regularization parameter \(\lambda = 4\) and kernel \(\kappa(\vec x, \vec x') = (1 + \vec x \cdot\vec x')^2\):
\(\nvec{x}{1} = (1, 2, 0)\), \(y_1 = 1\)\(\nvec{x}{2} = (0, 1, 2)\), \(y_2 = -1\)\(\nvec{x}{3} = (2, 0, 2)\), \(y_3 = 1\)\(\nvec{x}{4} = (1, 0, 1)\), \(y_4 = -1\)\(\nvec{x}{5} = (0, 0, 0)\), \(y_5 = 1\) Suppose the solution to the dual problem is \(\vec\alpha = (2, 0, 1, -1, 2)\).
Consider a new point \(\vec x = (1, 1, 1)\). What is \(H(\vec x)\)?
Solution
Video explanation: https://youtu.be/miyY9BeL0QI
Problem #096
Tags: Gaussians
Recall that the density of a \(d\)-dimensional ``axis-aligned'' Gaussian (that is, a Gaussian with diagonal covariance matrix \(C\)) is given by:
Consider the marginal density \(p_1(x_1)\), which is the density of the first coordinate, \(x_1\), of a \(d\)-dimensional axis-aligned Gaussian.
True or False: \(p_1(x_1)\) must be a Gaussian density.
Solution
True. Video explanation: https://youtu.be/5ZJ6ZIvgMGk
Problem #097
Tags: naive bayes
Consider the below data set collecting information on a set of 10 flowers.

What species does a Naive Bayes classifier predict for a flower with 3 petals and no leaves?
Solution
B. Video explanation: https://youtu.be/iKPAhJJcu6s
Problem #098
Tags: conditional independence
Suppose Justin has a dartboard at home that looks like the below:
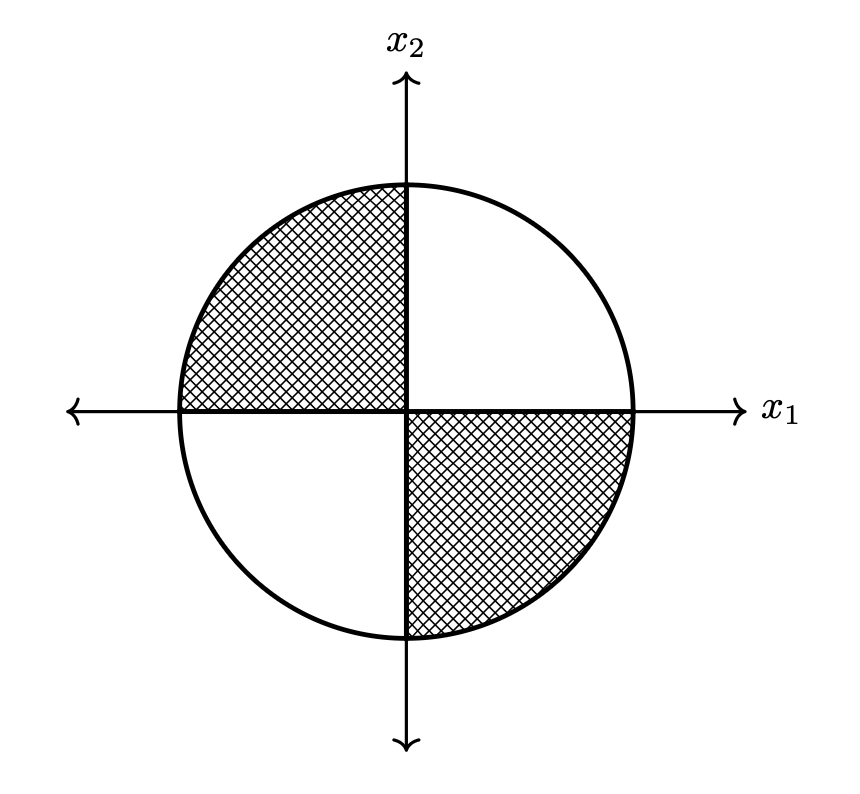
Justin uses the dartboard to determine how long the midterm will be: if he throws a dart and it lands in the shaded region, the midterm will have 17 questions; if it lands in the unshaded region, it will have 16 questions.
Assume that Justin's dart throws are drawn from a uniform distribution on the dartboard, and that the dart always hits the board (that is, the density function is constant everywhere on the dartboard, and zero off of the dartboard). Let \(X_1\) be the horizontal component of a dart throw and \(X_2\) be the vertical component. Let \(Q\) be the number of questions on the exam; since it is chosen randomly, it is also a random number.
Part 1)
True or False: \(X_1\) and \(X_2\) are independent.
Solution
False.
Part 2)
True or False: \(X_1\) and \(X_2\) are conditionally independent given \(Q\).
Solution
False.
Part 3)
True or False: \(X_1\) and \(Q\) are independent.
Solution
True.
Part 4)
True or False: \(X_1\) and \(Q\) are conditionally independent given \(X_2\).
Solution
False.
Solution
Video explanation: https://youtu.be/b4XlZsePCgU
Problem #099
Tags: Gaussians, linear and quadratic discriminant analysis
Suppose the underlying class-conditional densities in a binary classification problem are known to be multivariate Gaussians.
Suppose a Quadratic Discriminant Analysis (QDA) classifier using full covariance matrices for each class is trained on a data set of \(n\) points sampled from these densities.
True or False: As the size of the data set grows (that is, as \(n \to\infty\)), the training error of the QDA classifier must approach zero.
Solution
False. Video explanation: https://youtu.be/t40ex-JCYLY
Problem #100
Tags: Gaussians, maximum likelihood
Suppose a univariate Gaussian density function \(\hat f\) is fit to a set of data using the method of maximum likelihood estimation (MLE).
True or False: \(\hat f\) must be between 0 and 1 everywhere. That is, it must be the case that for every \(x \in\mathbb R\), \(0 < \hat f(x) \leq 1\).
Solution
False. Video explanation: https://youtu.be/zvpLrG4FYEc
Problem #101
Tags: linear and quadratic discriminant analysis
Suppose Quadratic Discriminant Analysis (QDA) is used to train a classifier on the following data set of \((x_i, y_i)\) pairs, where \(x_i\) is the feature and \(y_i\) is the class label:
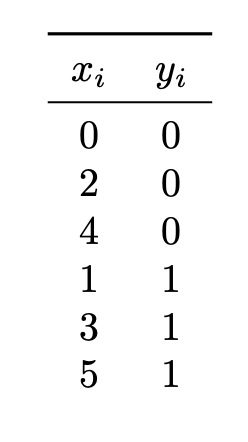
Univariate Gaussians are used to model the class conditional densities, each with their own mean and variance.
What is the prediction of the QDA classifier at \(x = 2.25\)?
Solution
Class 0.
Video explanation: https://youtu.be/5VxizVoBHsA
Problem #102
Tags: maximum likelihood
Consider Justin's rectangle density. It is a parametric density with two parameters, \(\alpha\) and \(\beta\), and pdf:
A picture of the density is shown below for convenience:
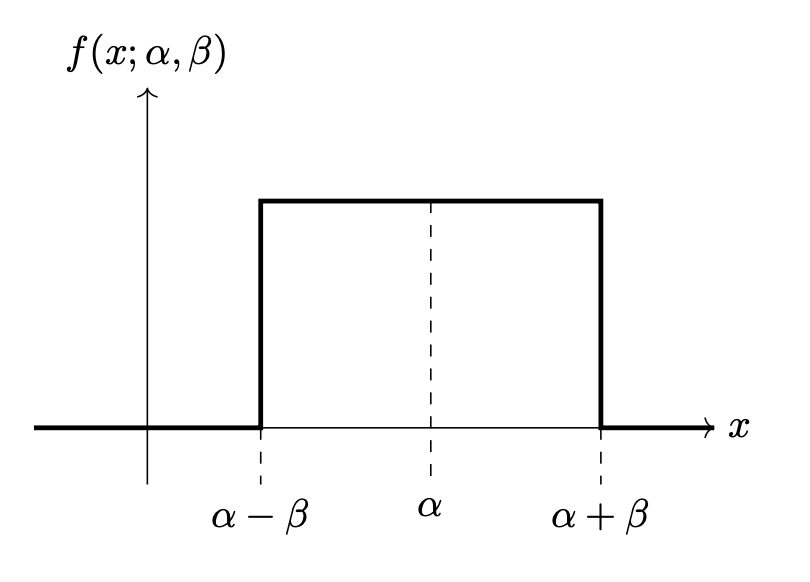
In all of the below parts, let \(\mathcal X = \{1, 2, 3, 6, 9\}\) be a data set of 5 points generated from the rectangle density.
Your answers to the below problems should all be in the form of a number. You may leave your answer as an unsimplified fraction or a decimal, if you prefer.
Part 1)
Let \(\mathcal L(\alpha, \beta; \mathcal X)\) be the likelihood function (with respect to the data given above). What is \(\mathcal L(6, 5)\)? Note that \(\mathcal L\) is the likelihood, not the log-likelihood.
Part 2)
What is \(\mathcal L(3, 2)\)?
Part 3)
What are the maximum likelihood estimates of \(\alpha\) and \(\beta\)?
\(\alpha\): \(\beta\):
Solution
Video explanation: https://youtu.be/loc1xv2QNJk
Problem #103
Tags: covariance, object type
Part 1)
Let \(\mathcal{X}\) be a data set of \(n\) points in \(\mathbb{R}^d\), and let \(\vec\alpha\) be the solution to the kernel ridge regression dual problem. What type of object is \(\vec\alpha\)?
Solution
B.
Part 2)
Suppose \(\nvec{x}{1}, \ldots, \nvec{x}{n}\) is a set of \(n\) points in \(\mathbb{R}^d\), \(y_1, \ldots, y_n\) is a set of \(n\) labels (each either \(-1\) or \(1\)), \(\vec w\) is a \(k\)-dimensional vector, and \(\lambda\) is a scalar.
Let \(\vec\phi : \mathbb{R}^d \to\mathbb{R}^k\) be a feature map.
What type of object is the following?
Solution
D.
Part 3)
Let \(\nvec{x}{1}, \ldots, \nvec{x}{n}\) be a set of \(n\) points in \(\mathbb{R}^d\). Let \(\vec\mu = \sum_{i=1}^n \nvec{x}{i}\) be the mean of the data set, and let \(C\) be the sample covariance matrix.
What type of object is the following?
Solution
A.
Part 4)
Let \(\nvec{x}{1}, \ldots, \nvec{x}{n}\) be a data set of \(n\) points in \(\mathbb{R}^d\) sampled from a multivariate Gaussian with known covariance matrix but unknown mean, \(\vec\mu\). Let \(\mathcal L(\vec\mu)\) be the likelihood function for the Gaussian's mean, \(\vec\mu\). What type of object is \(\mathcal L\)?
Solution
Video explanation: https://youtu.be/wr8sNCEiIQs
Problem #104
Tags: histogram estimators
Let \((\nvec{x}{1}, y_1), \ldots, (\nvec{x}{n}, y_n)\) be a set of \(n\) points in a binary classification problem, where \(\nvec{x}{i}\in\mathbb{R}^2\) and \(y_i \in\{0, 1\}\).
Suppose a classifier is trained by estimating the class-conditional densities with histograms using rectangular bins and applying the Bayes classification rule.
True or False: it is always possible to achieve a 100\% training accuracy with this classifier by choosing the rectangular bins to be sufficiently small. You may assume that no two points \(\nvec{x}{i}\) and \(\nvec{x}{j}\) are identical.
Solution
True. Video explanation: https://youtu.be/A1fBjOnjs5E
Problem #105
Tags: naive bayes
Does standardizing the data possibly change the prediction made by Gaussian Naive Bayes?
More precisely, let \((\nvec{x}{1}, y_1), \ldots, (\nvec{x}{n}, y_n)\) be a set of training data for a binary classification problem, where each \(\nvec{x}{i}\in\mathbb R^d\) and each \(y_i \in\{0, 1\}\). Suppose that when a Gaussian Na\"ive Bayes classifier is trained on this data set, \(\nvec{x}{1}\) is predicted to be from Class \(0\).
Now suppose that the data set is standardized by subtracting the mean of each feature and dividing by its standard deviation. This is done for the data set as a whole, not separately for each class. Let \(\nvec{z}{1}, \ldots, \nvec{z}{n}\) be the standardized data set.
True or False: when a Gaussian Na\"ive Bayes classifier is trained on the standardized data set, it must still predict \(\nvec{z}{1}\) to be from Class \(0\).
Solution
True.
Video explanation: https://youtu.be/hGlWsEk_tYI
Problem #106
Tags: covariance, maximum likelihood
Consider the following set of 6 data points:
In the below parts, your answers should be given as numbers. You may leave your answer as an unsimplified fraction or a decimal, if you prefer.
Part 1)
What is the (1,2) entry of the sample covariance matrix?
Part 2)
What is the (2,2) entry of the sample covariance matrix?
Solution
Video explanation: https://youtu.be/BvFKfpGVR9k
Problem #107
Tags: covariance, Gaussians
The picture below shows the contours of a multivariate Gaussian density function:
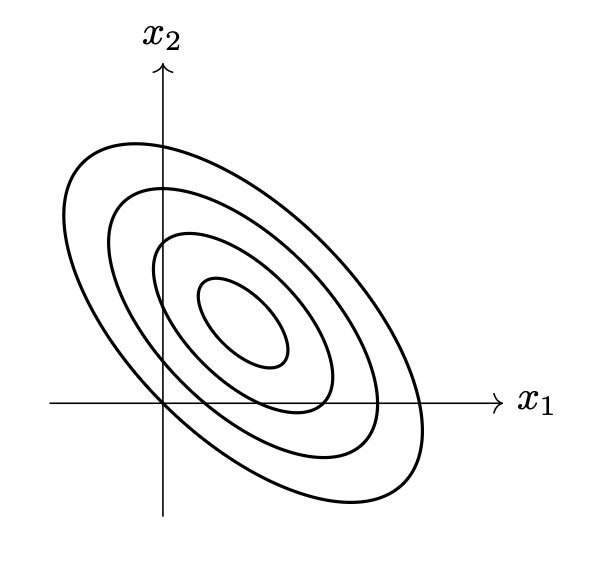
Which one of the following could possibly be the covariance matrix of this Gaussian?
Solution
C. Video explanation: https://youtu.be/5b1nzF0yYeE
Problem #108
Tags: linear and quadratic discriminant analysis
The picture below shows the decision boundary of a binary classifier. The shaded region is where the classifier predicts for Class 1; everywhere else, the classifier predicts for Class 0.
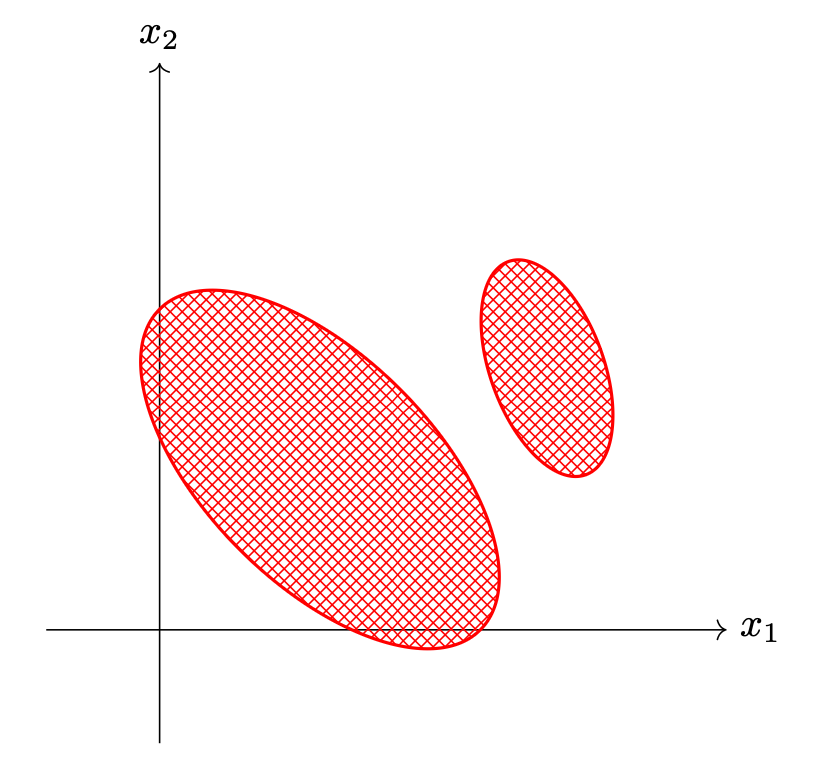
True or False: this could be the decision boundary of a Quadratic Discriminant Analysis (QDA) classifier that models the class-conditional densities as multivariate Gaussians with full covariance matrices.
Solution
False. Video explanation: https://youtu.be/fQm3_JcpVys
Problem #109
Tags: kernel ridge regression
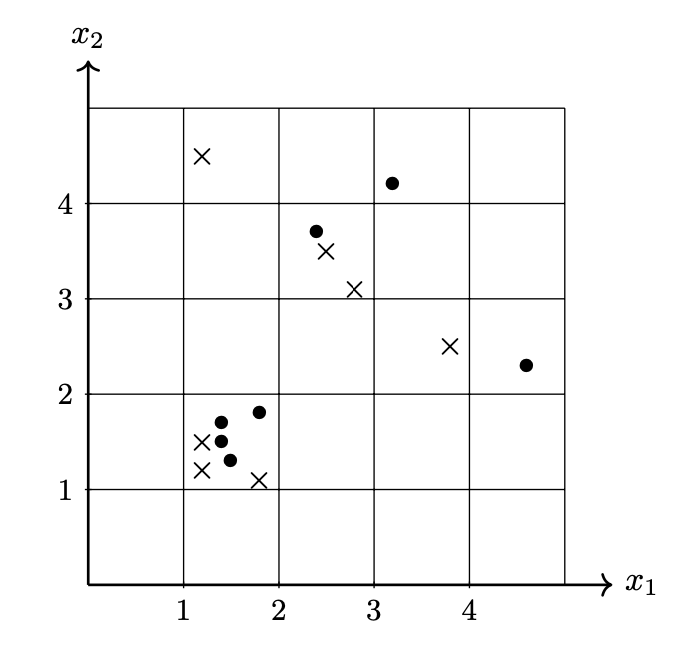
Consider the following data set of four points whose feature vectors are in \(\mathbb{R}^2\) and whose labels are in \(\{-1,1\}\):
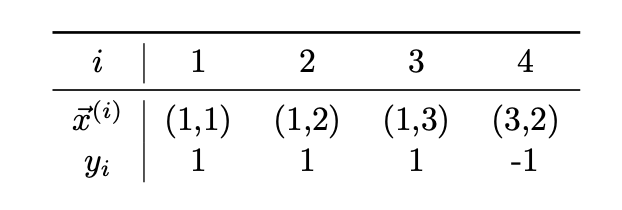
For convenience, we've plotted the data below. Each point is labeled with either the positive class (denoted by \(\times\)) or the negative class (denoted by \(\bullet\)).
Suppose an unnamed kernel classifier \(H(\vec x) = \sum_{i=1}^n \alpha_i \kappa(\nvec{x}{x}, \vec x)\) has been trained on this data using a (spherical) Gaussian kernel and kernel width parameter \(\gamma = 1\). Suppose the solution to the dual problem is found to be \(\vec\alpha = (1, 1, 1, -3)^T\).
What class will the classifier predict for the point \((2,2)\)? For convenience, we've plotted this point on the graph above as a question mark.
Solution
-1 (the \(\bullet\) class).
Problem #110
Tags: bayes error, bayes classifier
Shown below are two conditional densities, \(p_1(x \,|\, Y = 1)\) and \(p_0(x \given Y = 0)\), describing the distribution of a continuous random variable \(X\) for two classes: \(Y = 0\)(the solid line) and \(Y = 1\)(the dashed line). You may assume that both densities are piecewise constant.
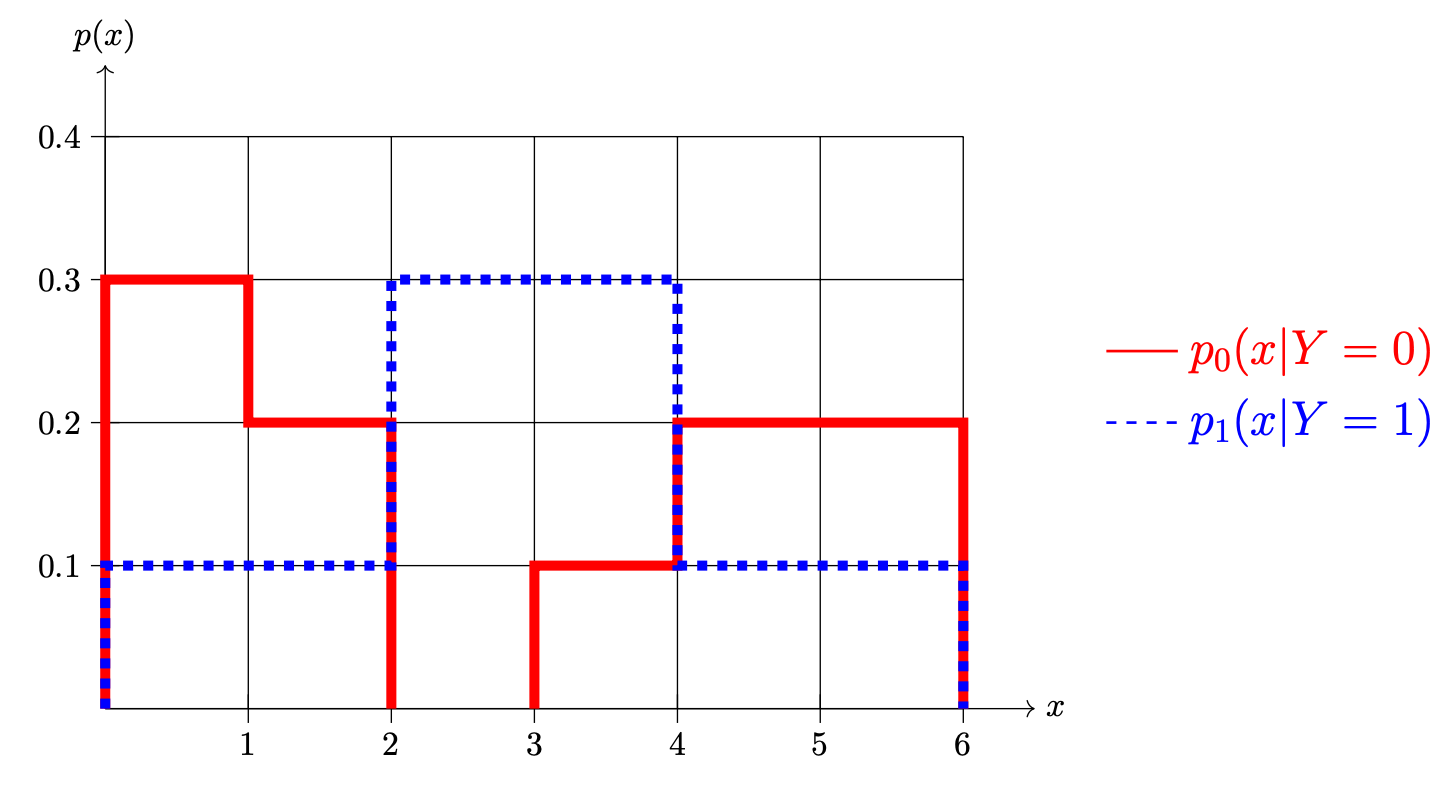
Part 1)
Suppose that \(\pr(Y = 1) = \pr(Y = 0) = 0.5\). What is \(\pr(1 \leq X \leq 3)\)?
Part 2)
Suppose \(\pr(Y = 1) = \pr(Y = 0) = 0.5\). What is the prediction of the Bayes classifier at \(x = 1.5\)?
Solution
Class 0.
Part 3)
Suppose again that \(\pr(Y = 1) = \pr(Y = 0) = 0.5\). What is the Bayes error with respect to this distribution?
Part 4)
Now suppose \(\pr(Y = 1) = 0.7\) and \(\pr(Y = 0) = 0.3\). What is \(\pr(1 \leq X \leq 3)\)?
Part 5)
Suppose again that \(\pr(Y = 1) = 0.7\) and \(\pr(Y = 0) = 0.3\). What is the prediction of the Bayes classifier at \(x = 1.5\)?
Solution
Class 1.
Part 6)
Suppose again that \(\pr(Y = 1) = 0.7\) and \(\pr(Y = 0) = 0.3\). What is the Bayes error with respect to this distribution?
Problem #111
Tags: bayes classifier, histogram estimators
In this problem, consider the following labeled data set of 19 points, 7 from Class 1 and 12 from Class 0.

Suppose the class conditional densities are estimated using a histogram estimator with bins: \([0, .25), [.25, .5), [.5, 75),\) and \([.75, 1.0)\).
In all of the parts below, you may write your answer either as a decimal or as a fraction.
Part 1)
What is the estimate of the Class 0 density at \(x = 0.6\)? That is, what is the estimate \(\hat p(0.6 \given Y = 0)\)?
Part 2)
Using the same histogram estimator, what is the estimate \(\hat\pr(Y = 1 \given x = 0.35)\)?
Part 3)
What is the estimate of the marginal density of \(x\) at \(x = 0.1\)? That is, what is \(\hat p(0.1)\)?
Part 4)
Let \(\hat p(x \given Y = 0)\) be the histogram density estimate for the Class 0 conditional density. What is
Problem #112
Tags: kernel ridge regression
Suppose a prediction function \(H(\vec x)\) is trained using kernel ridge regression on the data below using regularization parameter \(\lambda = 4\) and kernel \(\kappa(\vec x, \vec x') = (1 + \vec x \cdot\vec x')^2\):
\(\nvec{x}{1} = (0, 1, 1)\), \(y_1 = 1\)\(\nvec{x}{2} = (1, 1, 1)\), \(y_2 = -1\)\(\nvec{x}{3} = (2, 2, 2)\), \(y_3 = 1\)\(\nvec{x}{4} = (1, 1, 0)\), \(y_4 = -1\)\(\nvec{x}{5} = (0, 1, 0)\), \(y_5 = 1\) Suppose the solution to the dual problem is \(\vec\alpha = (-1, 1, 0, 3, -2)\).
Consider a new point \(\vec x = (2, 0, 1)^T\). What is \(H(\vec x)\)?
Problem #113
Tags: covariance, maximum likelihood
Consider the following set of 6 data points:
In the below parts, your answers should be given as numbers. You may leave your answer as an unsimplified fraction or a decimal, if you prefer.
Part 1)
What is the (1,3) entry of the sample covariance matrix?
Part 2)
What is the (1,2) entry of the sample covariance matrix?
Problem #114
Tags: conditional independence, Gaussians, covariance
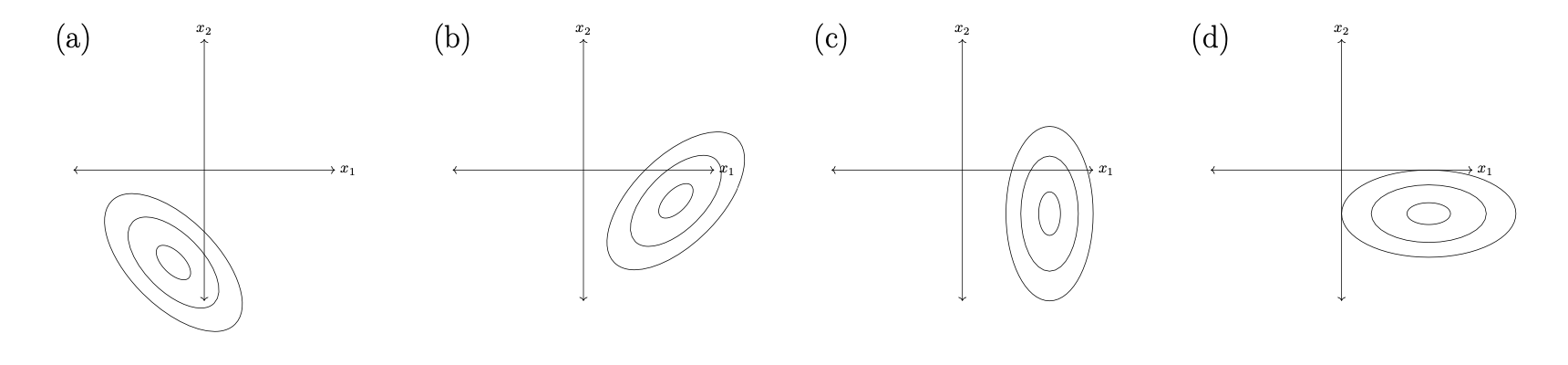
Let \(X_1\) and \(X_2\) be two independent random variables. Suppose the distribution of \(X_1\) has the Gaussian density:
while the distribution of \(X_2\) has the Gaussian density:
Which one of the following pictures shows the contours of the joint density \(p(x_1, x_2)\)(the density for the joint distribution of \(X_1\) and \(X_2\))?
Solution
Picture (d).
Problem #115
Tags: Gaussians, maximum likelihood
Suppose it is known that the distribution of a random variable \(X\) has a univariate Gaussian density function \(f\).
True or False: \(f\) must be between 0 and 1 everywhere. That is, it must be the case that for every \(x \in\mathbb R\), \(0 < f(x) \leq 1\).
Solution
False.
Problem #116
Tags: covariance, Gaussians, bayes error
Suppose that, in a binary classification setting, the true underlying class-conditional densities \(p(\vec x \given Y=0)\) and \(p(\vec x \given Y=1)\) are known to each be multivariate Gaussians with full covariance matrices. Suppose, also, that \(\pr(Y = 1) = \pr(Y = 0) = \frac{1}{2}\).
True or False: it is possible that the Bayes error in this case is exactly zero.
Solution
False.
Problem #119
Tags: histogram estimators
Consider the following data set of 14 points in \(\mathbb R^2\). Each point has a label in \(\{ 1, -1 \}\). Points from Class 1 are marked with \(\times\) and points from Class -1 are marked with \(\bullet\).
Suppose the class-conditional density estimates are computed from this data using a histogram density estimator using the \(1 \times 1\) bins shown in the figure above.
If these estimates are used in place of the true class-conditional densities in the Bayes classifier, what will be the training error of the classifier? That is, what percentage of the data above will be misclassified? You may leave your answer as a fraction or a decimal.
Problem #120
Tags: covariance, Gaussians
The picture below shows the contours of a multivariate Gaussian density function:
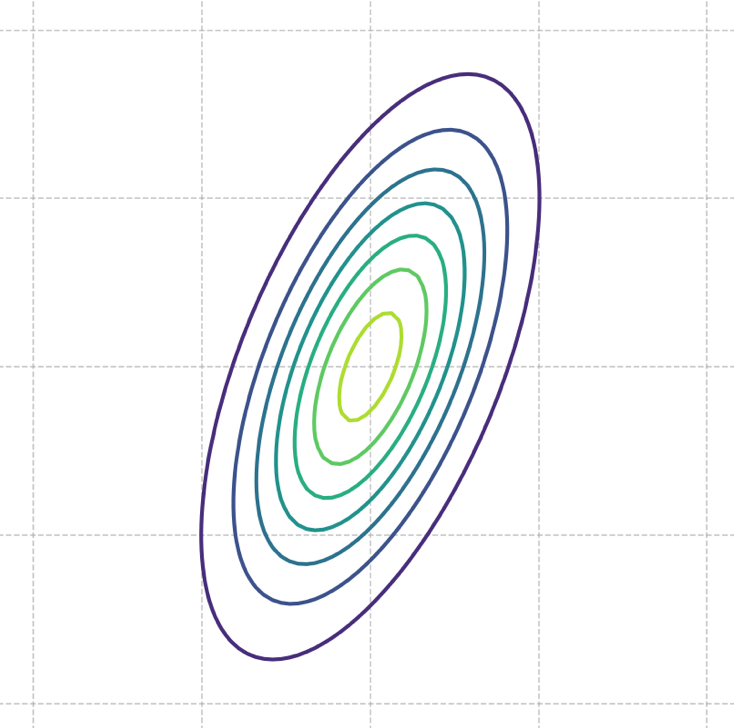
Which one of the following could possibly be the covariance matrix of this Gaussian?
Solution
C.
Problem #121
Tags: linear and quadratic discriminant analysis
The picture below shows the decision boundary of a binary classifier. The shaded region is where the classifier predicts for Class 1; everywhere else, the classifier predicts for Class 0. You can assume that the shaded region extends infinitely to the left and down.

True or False: this could be the decision boundary of a classifier that estimates each class conditional density using two Gaussians with different means but the same, shared full covariance matrix, and applies the Bayes classification rule.
Solution
False.
Problem #122
Tags: conditional independence
Suppose that Justin has a wall at home that he has painted to look like the below:
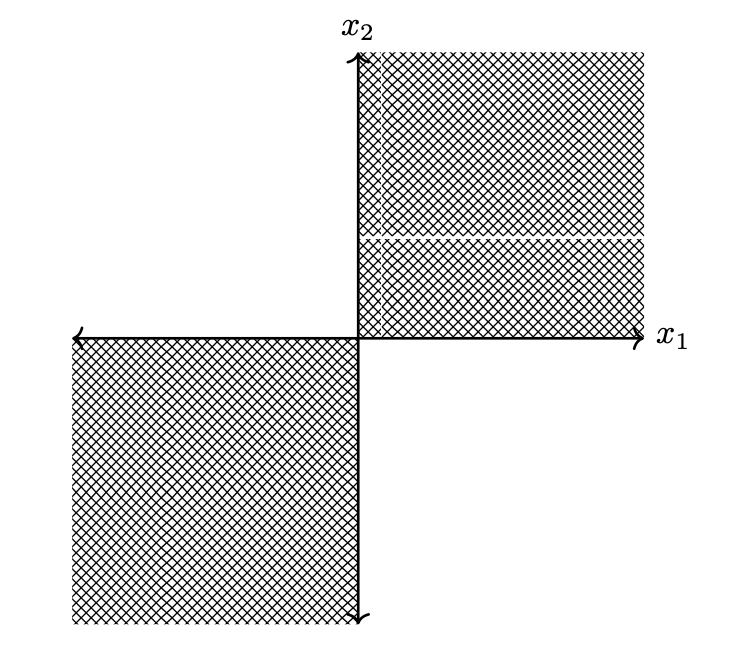
Justin uses the wall to determine how long Redemption Midterm 02 will be: if he throws a dart at the origin and it lands in the shaded region, the redemption midterm will have 14 questions; if it lands in the unshaded region, it will have 2 questions.
Assume that Justin's dart throws are drawn from a spherical Gaussian whose mean is at the origin. Let \(X_1\) be the horizontal component of a dart throw and \(X_2\) be the vertical component. Let \(Q\) be the number of questions on the exam; since it is chosen randomly, it is also a random number. You can assume that the wall is infinitely large, and that the shaded regions extend infinitely up and to the right, and down and to the left.
Part 1)
True or False: \(X_1\) and \(X_2\) are independent.
Solution
True.
Part 2)
True or False: \(X_1\) and \(X_2\) are conditionally independent given \(Q\).
Solution
False.
Part 3)
Let \(D = \sqrt{X_1^2 + X_2^2}\), and note that \(D\) is the distance of a dart throw from the origin. True or False: \(D\) and \(Q\) are independent.
Solution
True.
Part 4)
True or False: \(X_1\) and and \(X_2\) are conditionally independent given \(D\).
Solution
False.