Problems tagged with "Gaussians"
Problem #040
Tags: Gaussians, maximum likelihood
Suppose a Gaussian with a diagonal covariance matrix is fit to 200 points in \(\mathbb R^4\) using the maximum likelihood estimators. How many parameters are estimated? Count each entry of \(\mu\) and the covariance matrix that must be estimated as its own parameter.
Problem #050
Tags: Gaussians
Suppose data points \(x_1, \ldots, x_n\) are independently drawn from a univariate Gaussian distribution with unknown parameters \(\mu\) and \(\sigma\).
True or False: it is guaranteed that, given enough data (that is, \(n\) large enough), a univariate Gaussian fit to the data using the method of maximum likelihood will approximate the true underlying density arbitrarily closely.
Solution
True.
Problem #053
Tags: Gaussians, maximum likelihood
Suppose a Gaussian with a diagonal covariance matrix is fit to 200 points in \(\mathbb R^4\) using the maximum likelihood estimators. How many parameters are estimated? Count each entry of \(\vec\mu\) and the covariance matrix that must be estimated as its own parameter (the off-diagonal elements of the covariance are zero, and shouldn't be included in your count).
Problem #054
Tags: Gaussians
Let \(f_1\) be a univariate Gaussian density with parameters \(\mu\) and \(\sigma_1\). And let \(f_2\) be a univariate Gaussian density with parameters \(\mu\) and \(\sigma_2 \neq\sigma_1\). That is, \(f_2\) is centered at the same place as \(f_1\), but with a different variance.
Consider the density \(f(x) = \frac{1}{2}(f_1(x) + f_2(x))\); the factor of \(1/2\) is a normalization factor which ensures that \(f\) integrates to one.
True or False: \(f\) must also be a Gaussian density.
Solution
False. The sum of two Gaussian densities is not necessarily a Gaussian density, even if the two Gaussians have the same mean.
If you try adding two Gaussian densities with different variances, you will get:
For this to be a Gaussian, we'd need to be able to write it in the form:
but this is not possible when \(\sigma_1 \neq\sigma_2\).
Problem #096
Tags: Gaussians
Recall that the density of a \(d\)-dimensional ``axis-aligned'' Gaussian (that is, a Gaussian with diagonal covariance matrix \(C\)) is given by:
Consider the marginal density \(p_1(x_1)\), which is the density of the first coordinate, \(x_1\), of a \(d\)-dimensional axis-aligned Gaussian.
True or False: \(p_1(x_1)\) must be a Gaussian density.
Solution
True. Video explanation: https://youtu.be/5ZJ6ZIvgMGk
Problem #099
Tags: Gaussians, linear and quadratic discriminant analysis
Suppose the underlying class-conditional densities in a binary classification problem are known to be multivariate Gaussians.
Suppose a Quadratic Discriminant Analysis (QDA) classifier using full covariance matrices for each class is trained on a data set of \(n\) points sampled from these densities.
True or False: As the size of the data set grows (that is, as \(n \to\infty\)), the training error of the QDA classifier must approach zero.
Solution
False. Video explanation: https://youtu.be/t40ex-JCYLY
Problem #100
Tags: Gaussians, maximum likelihood
Suppose a univariate Gaussian density function \(\hat f\) is fit to a set of data using the method of maximum likelihood estimation (MLE).
True or False: \(\hat f\) must be between 0 and 1 everywhere. That is, it must be the case that for every \(x \in\mathbb R\), \(0 < \hat f(x) \leq 1\).
Solution
False. Video explanation: https://youtu.be/zvpLrG4FYEc
Problem #107
Tags: covariance, Gaussians
The picture below shows the contours of a multivariate Gaussian density function:
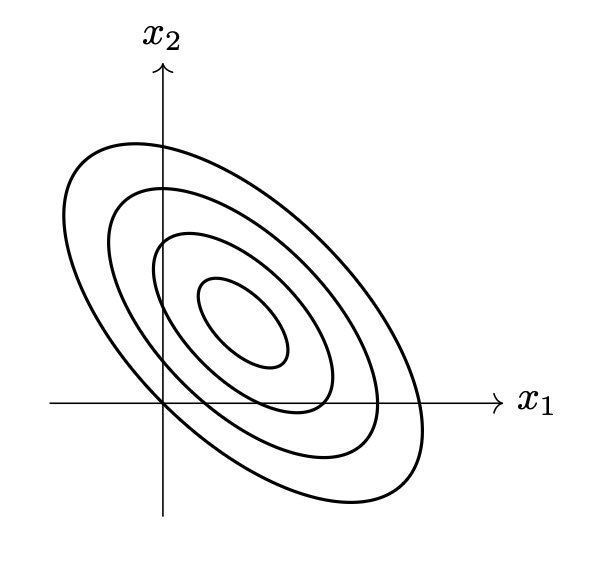
Which one of the following could possibly be the covariance matrix of this Gaussian?
Solution
C. Video explanation: https://youtu.be/5b1nzF0yYeE
Problem #114
Tags: conditional independence, Gaussians, covariance
Let \(X_1\) and \(X_2\) be two independent random variables. Suppose the distribution of \(X_1\) has the Gaussian density:
while the distribution of \(X_2\) has the Gaussian density:
Which one of the following pictures shows the contours of the joint density \(p(x_1, x_2)\)(the density for the joint distribution of \(X_1\) and \(X_2\))?
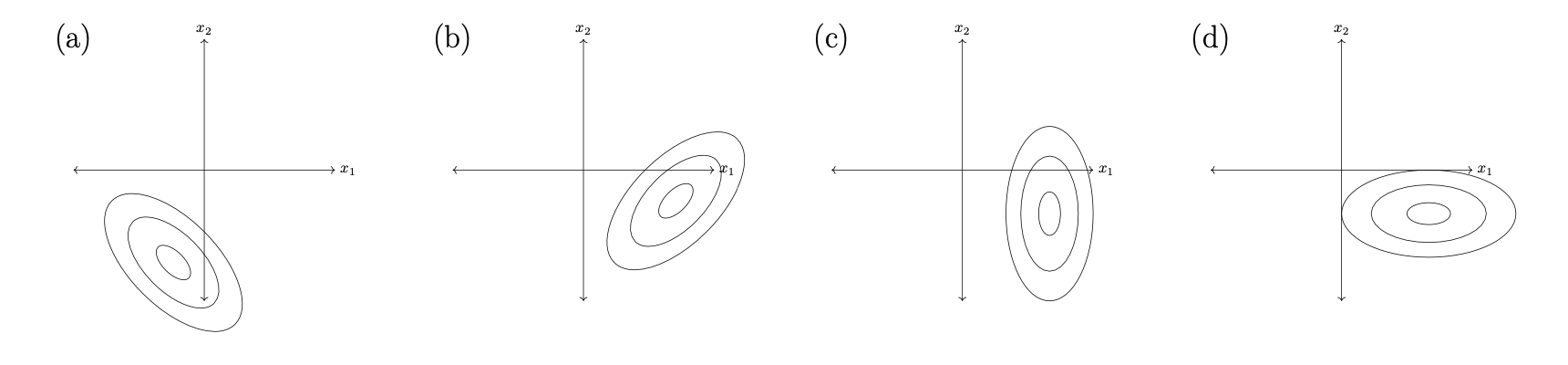
Solution
Picture (d).
Problem #115
Tags: Gaussians, maximum likelihood
Suppose it is known that the distribution of a random variable \(X\) has a univariate Gaussian density function \(f\).
True or False: \(f\) must be between 0 and 1 everywhere. That is, it must be the case that for every \(x \in\mathbb R\), \(0 < f(x) \leq 1\).
Solution
False.
Problem #116
Tags: covariance, Gaussians, bayes error
Suppose that, in a binary classification setting, the true underlying class-conditional densities \(p(\vec x \given Y=0)\) and \(p(\vec x \given Y=1)\) are known to each be multivariate Gaussians with full covariance matrices. Suppose, also, that \(\pr(Y = 1) = \pr(Y = 0) = \frac{1}{2}\).
True or False: it is possible that the Bayes error in this case is exactly zero.
Solution
False.
Problem #120
Tags: covariance, Gaussians
The picture below shows the contours of a multivariate Gaussian density function:
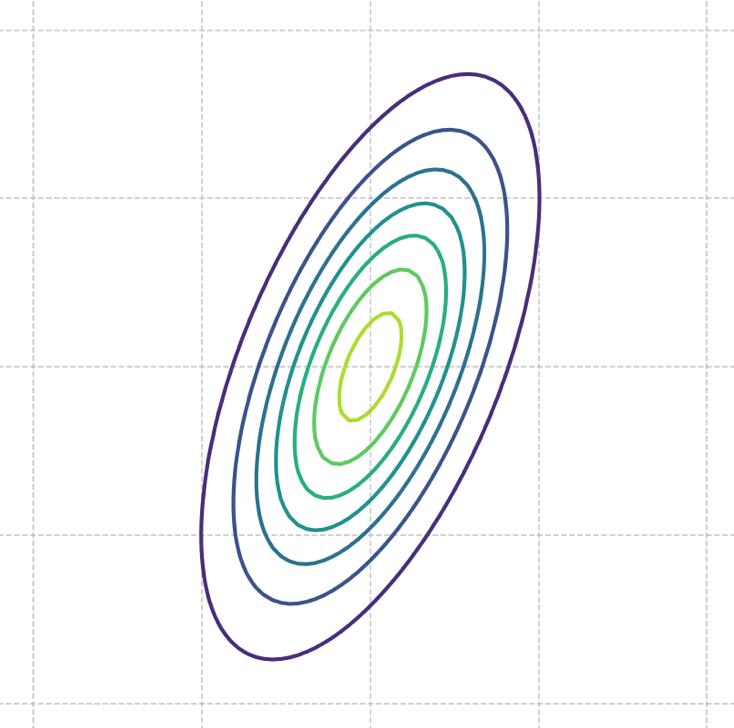
Which one of the following could possibly be the covariance matrix of this Gaussian?
Solution
C.