Problems tagged with "covariance"
Problem #038
Tags: covariance
Consider a data set of \(n\) points in \(\mathbb R^d\), \(\nvec{x}{1}, \ldots, \nvec{x}{n}\). Suppose the data are standardized, creating a set of new points \(\nvec{z}{1}, \ldots, \nvec{z}{n}\). That is, if the new points are stacked into an \(n \times d\) matrix, \(Z\), the mean and variance of each column of \(Z\) would be zero and one, respectively.
True or False: the covariance matrix of the standardized data must be the \(d\times d\) identity matrix; that is, the \(d \times d\) matrix with ones along the diagonal and zeros off the diagonal.
Solution
False.
Problem #041
Tags: covariance
Suppose a data set consists of the following three measurements for each Saturday last year: \(X_1\): The day's high temperature \(X_2\): The number of people at Pacific Beach on that day \(X_3\): The number of people wearing coats on that day
Suppose the covariance between these features is calculated and placed into a \(3 \times 3\) sample covariance matrix, \(C\). Which of the below options most likely shows the sign of each entry of the sample covariance matrix?
Solution
The second option.
Problem #042
Tags: covariance
Suppose we have two data sets, \(\mathcal{D}_1\) and \(\mathcal{D}_2\), each containing \(n/2\) points in \(\mathbb R^d\). Let \(\nvec{\mu}{1}\) and \(C^{(1)}\) be the mean and sample covariance matrix of \(\mathcal{D}_1\), and let \(\nvec{\mu}{2}\) and \(C^{(2)}\) be the mean and sample covariance matrix of \(\mathcal{D}_2\).
Suppose the two data sets are combined into a single data set \(\mathcal D\) containing \(n\) points.
Part 1)
True or False: the mean of the combined data \(\mathcal{D}\) is equal to \(\displaystyle\frac{\nvec{\mu}{1} + \nvec{\mu}{2}}{2}\).
Solution
True.
Part 2)
True or False: the sample covariance matrix of the combined data \(\mathcal{D}\) is equal to \(\displaystyle\frac{C^{(1)} + C^{(2)}}{2}\).
Solution
False
Problem #043
Tags: covariance
Suppose a random vector \(\vec X = (X_1, X_2)\) has a multivariate Gaussian distribution. Suppose it is known that known that \(X_1\) and \(X_2\) are independent.
Let \(C\) be the Gaussian distribution's covariance matrix.
Part 1)
True or False: \(C\) must be diagonal.
Solution
True.
Part 2)
True or False: each entry of \(C\) must the same.
Solution
False.
Problem #052
Tags: covariance
Let \(\mathcal D\) be a set of data points in \(\mathbb R^d\), and let \(C\) be the sample covariance matrix of \(\mathcal D\). Suppose each point in the data set is shifted in the same direction and by the same amount. That is, suppose there is a vector \(\vec\delta\) such that if \(\nvec{x}{i}\in\mathcal D\), then \(\nvec{x}{i} + \vec\delta\) is in the new data set.
True or False: the sample covariance matrix of the new data set is equal to \(C\)(the sample covariance matrix of the original data set).
Solution
True.
Problem #055
Tags: covariance
Consider the data set \(\mathcal D\) shown below.
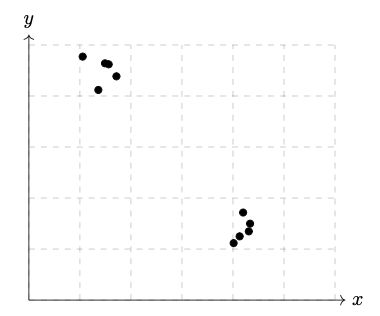
What will be the sign of the \((1,2)\) entry of the data's sample covariance matrix?
Solution
The sign will be negative.
Problem #103
Tags: covariance, object type
Part 1)
Let \(\mathcal{X}\) be a data set of \(n\) points in \(\mathbb{R}^d\), and let \(\vec\alpha\) be the solution to the kernel ridge regression dual problem. What type of object is \(\vec\alpha\)?
Solution
B.
Part 2)
Suppose \(\nvec{x}{1}, \ldots, \nvec{x}{n}\) is a set of \(n\) points in \(\mathbb{R}^d\), \(y_1, \ldots, y_n\) is a set of \(n\) labels (each either \(-1\) or \(1\)), \(\vec w\) is a \(k\)-dimensional vector, and \(\lambda\) is a scalar.
Let \(\vec\phi : \mathbb{R}^d \to\mathbb{R}^k\) be a feature map.
What type of object is the following?
Solution
D.
Part 3)
Let \(\nvec{x}{1}, \ldots, \nvec{x}{n}\) be a set of \(n\) points in \(\mathbb{R}^d\). Let \(\vec\mu = \sum_{i=1}^n \nvec{x}{i}\) be the mean of the data set, and let \(C\) be the sample covariance matrix.
What type of object is the following?
Solution
A.
Part 4)
Let \(\nvec{x}{1}, \ldots, \nvec{x}{n}\) be a data set of \(n\) points in \(\mathbb{R}^d\) sampled from a multivariate Gaussian with known covariance matrix but unknown mean, \(\vec\mu\). Let \(\mathcal L(\vec\mu)\) be the likelihood function for the Gaussian's mean, \(\vec\mu\). What type of object is \(\mathcal L\)?
Solution
Video explanation: https://youtu.be/wr8sNCEiIQs
Problem #106
Tags: covariance, maximum likelihood
Consider the following set of 6 data points:
In the below parts, your answers should be given as numbers. You may leave your answer as an unsimplified fraction or a decimal, if you prefer.
Part 1)
What is the (1,2) entry of the sample covariance matrix?
Part 2)
What is the (2,2) entry of the sample covariance matrix?
Solution
Video explanation: https://youtu.be/BvFKfpGVR9k
Problem #107
Tags: covariance, Gaussians
The picture below shows the contours of a multivariate Gaussian density function:
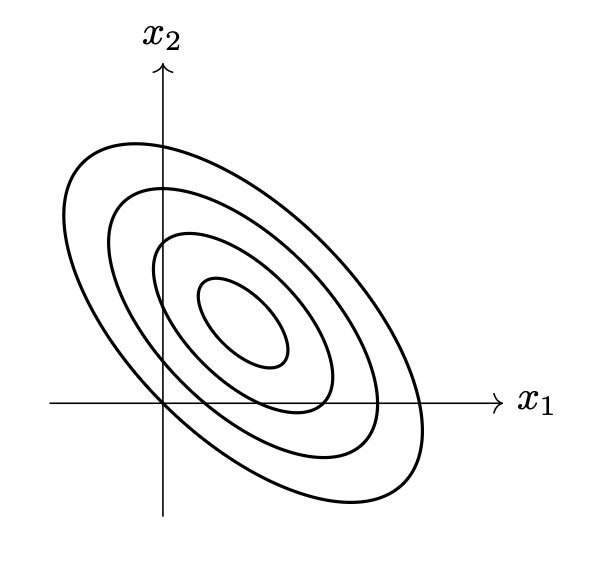
Which one of the following could possibly be the covariance matrix of this Gaussian?
Solution
C. Video explanation: https://youtu.be/5b1nzF0yYeE
Problem #113
Tags: covariance, maximum likelihood
Consider the following set of 6 data points:
In the below parts, your answers should be given as numbers. You may leave your answer as an unsimplified fraction or a decimal, if you prefer.
Part 1)
What is the (1,3) entry of the sample covariance matrix?
Part 2)
What is the (1,2) entry of the sample covariance matrix?
Problem #114
Tags: conditional independence, Gaussians, covariance
Let \(X_1\) and \(X_2\) be two independent random variables. Suppose the distribution of \(X_1\) has the Gaussian density:
while the distribution of \(X_2\) has the Gaussian density:
Which one of the following pictures shows the contours of the joint density \(p(x_1, x_2)\)(the density for the joint distribution of \(X_1\) and \(X_2\))?
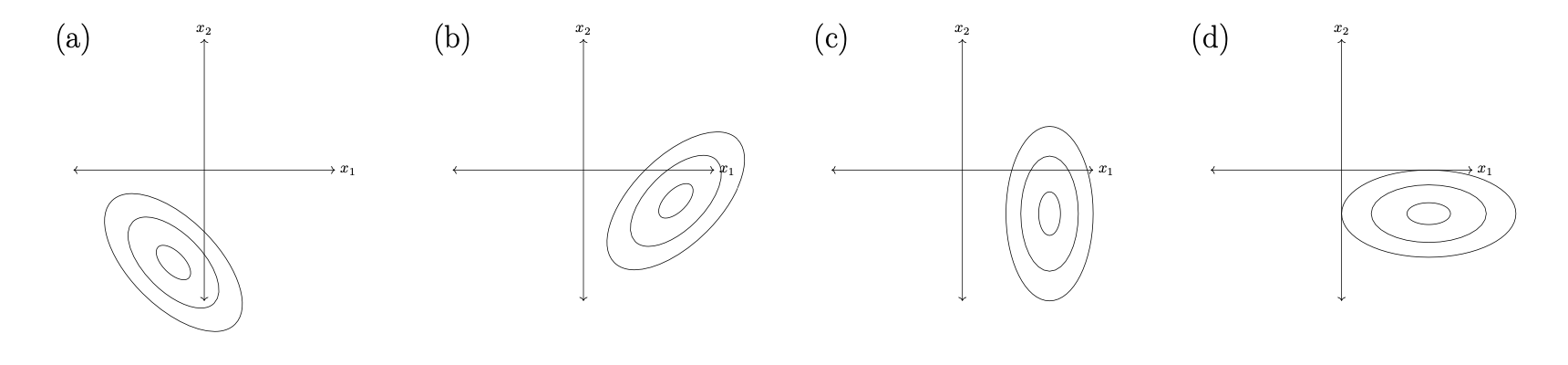
Solution
Picture (d).
Problem #116
Tags: covariance, Gaussians, bayes error
Suppose that, in a binary classification setting, the true underlying class-conditional densities \(p(\vec x \given Y=0)\) and \(p(\vec x \given Y=1)\) are known to each be multivariate Gaussians with full covariance matrices. Suppose, also, that \(\pr(Y = 1) = \pr(Y = 0) = \frac{1}{2}\).
True or False: it is possible that the Bayes error in this case is exactly zero.
Solution
False.
Problem #120
Tags: covariance, Gaussians
The picture below shows the contours of a multivariate Gaussian density function:
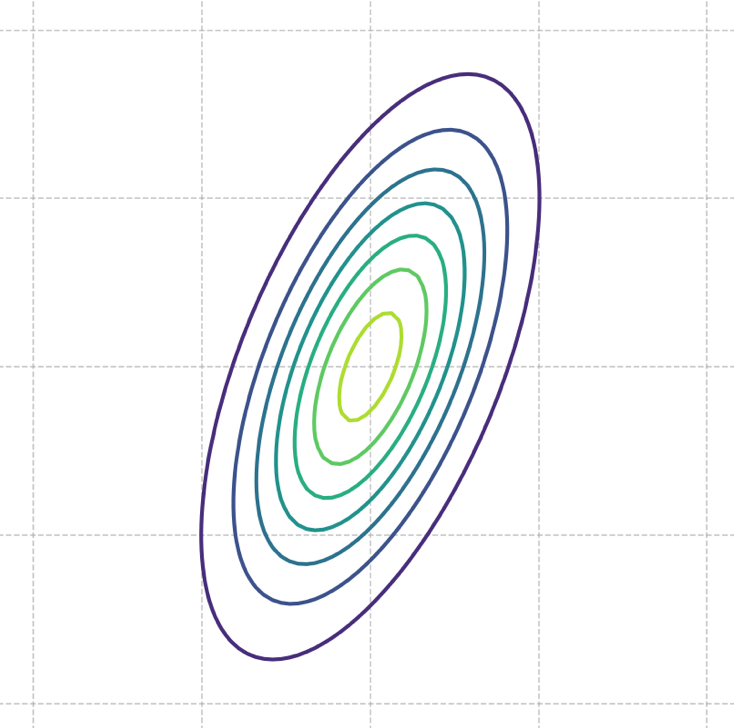
Which one of the following could possibly be the covariance matrix of this Gaussian?
Solution
C.