Problems tagged with "regularization"
Problem #015
Tags: regularization
Let \(R(\vec w)\) be the unregularized empirical risk with respect to the square loss (that is, the mean squared error) on a data set.
The image below shows the contours of \(R(\vec w)\). The dashed lines show places where \(\|\vec w\|_2\) is 2, 4, 6, etc.
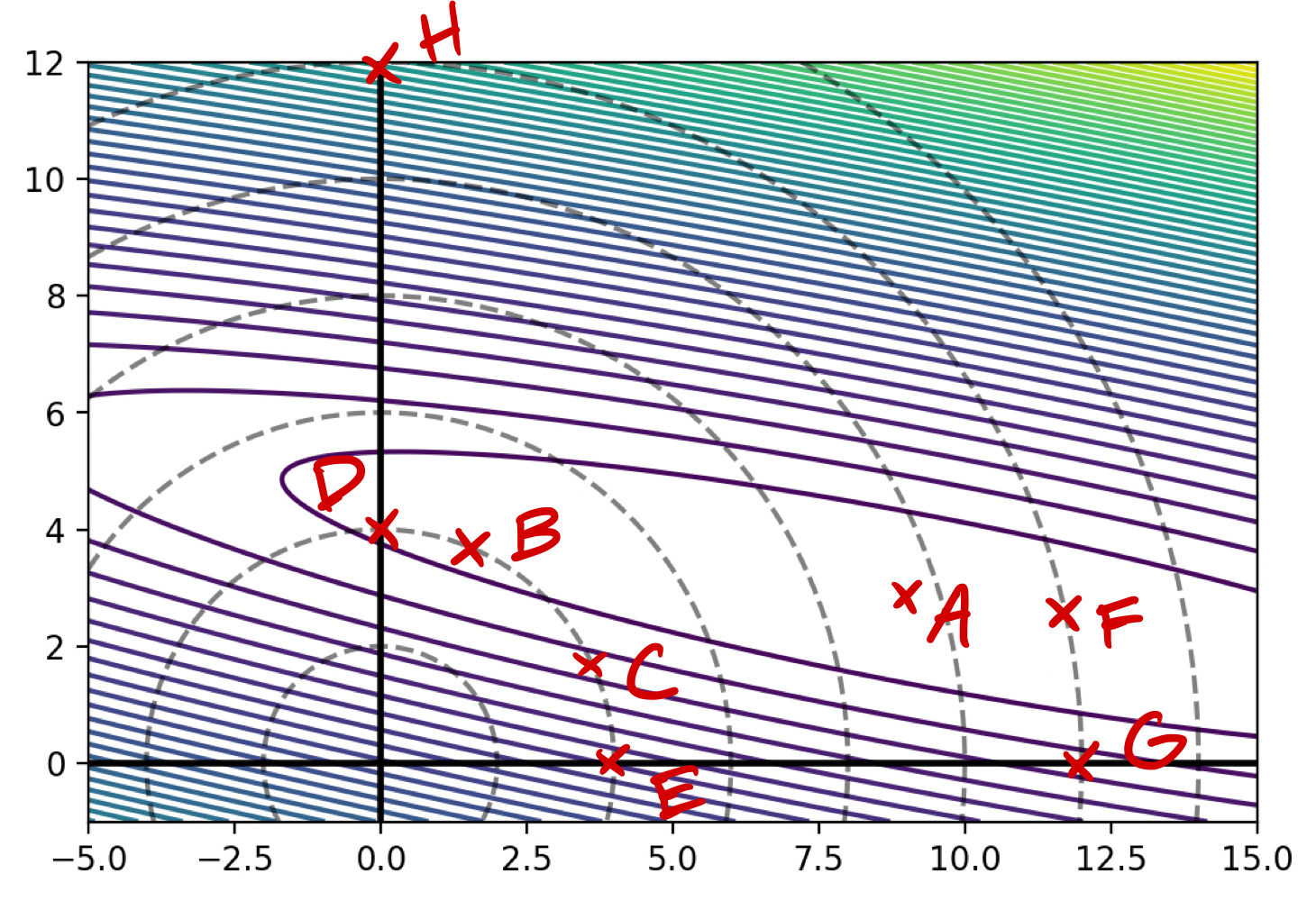
Part 1)
Assuming that one of the points below is the minimizer of the unregularized risk, \(R(\vec w)\), which could it possibly be?
Solution
A
Part 2)
Let the regularized risk \(\tilde R(\vec w) = R(\vec w) + \lambda\|\vec w \|_2^2\), where \(\lambda > 0\).
Assuming that one of the points below is the minimizer of the regularized risk, \(\tilde R(\vec w)\), which could it possibly be?
Solution
B
Problem #031
Tags: regularization
Let \(R(\vec w)\) be an unregularized empirical risk function with respect to some data set.
The image below shows the contours of \(R(\vec w)\). The dashed lines show places where \(\|\vec w\|_2\) is 1, 2, 3, etc.
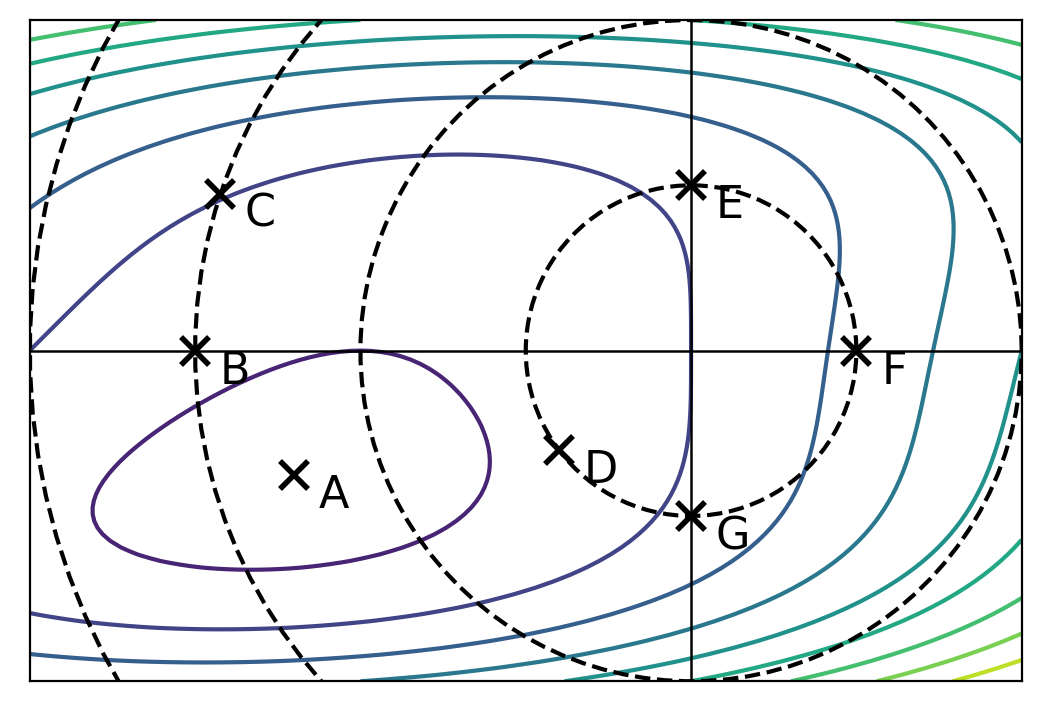
Part 1)
Assuming that one of the points below is the minimizer of the unregularized risk, \(R(\vec w)\), which could it possibly be?
Solution
A minimizer of the unregularized risk could be point A.
Part 2)
Let the regularized risk \(\tilde R(\vec w) = R(\vec w) + \lambda\|\vec w \|_2^2\), where \(\lambda > 0\).
Assuming that one of the points below is the minimizer of the regularized risk, \(\tilde R(\vec w)\), which could it possibly be?
Solution
A minimizer of the regularized risk could be point D.
Problem #070
Tags: regularization
Recall that in ridge regression, we solve the following optimization problem:
where \(\lambda > 0\) is a hyperparameter controlling the strength of regularization.
Suppose you solve the ridge regression problem with \(\lambda = 2\), and the resulting solution is the weight vector \(\vec w_\text{old}\). You then solve the ridge regression problem with \(\lambda = 4\) and find a weight vector \(\vec w_\text{new}\).
True or False: each component of the new solution, \(\vec w_\text{new}\), must be less than or equal to the corresponding component of the old solution, \(\vec w_\text{old}\).
Solution
False.
While it is true that \(\|\vec w_\text{new}\|\leq\|\vec w_\text{old}\|\), this does not imply that each component of \(\vec w_\text{new}\) is less than or equal to the corresponding component of \(\vec w_\text{old}\).
The picture to have in mind is that of the contour lines of the mean squared error (which are ovals), along with the circles representing where \(\|\vec w\| = c\) for some constant \(c\). The question asked us to consider going from \(\lambda = 2\) to \(\lambda = 4\), but to gain an intuition we can think of going from no regularization (\(\lambda = 0\)) to some regularization (\(\lambda > 0\)); this won't affect the outcome, but will make the story easier to tell.
Consider the situation shown below:

When we had no regularization, the solution was \(\vec w_\text{old}\), as marked. Suppose we add regularization, and we're told that the regularization is such that when we solve the ridge regression problem, the norm of \(\vec w_\text{new}\) will be equal to \(c\), and that the radius of the circle we've drawn is \(c\). Then the solution \(\vec w_\text{new}\) will be the point marked, since that is the point on the circle that is on the lowest contour.
Notice that the point \(\vec w_\text{new}\) is closer to the origin, and it's first component is much smaller than the first component of \(\vec w_\text{old}\). However, the second component of \(\vec w_\text{new}\) is actually larger than the second component of \(\vec w_\text{old}\).
Problem #075
Tags: regularization
The ``inifinity norm'' of a vector \(\vec w \in\mathbb R^d\), written \(\|\vec w\|_\infty\), is defined as:
That is, it is the maximum absolute value of any entry of \(\vec w\).
Let \(R(\vec w)\) be an unregularized risk function on a data set. The solid curves in the plot below are the contours of \(R(\vec w)\). The dashed lines show where \(\|\vec w\|_\infty\) is equal to 1, 2, 3, and so on.
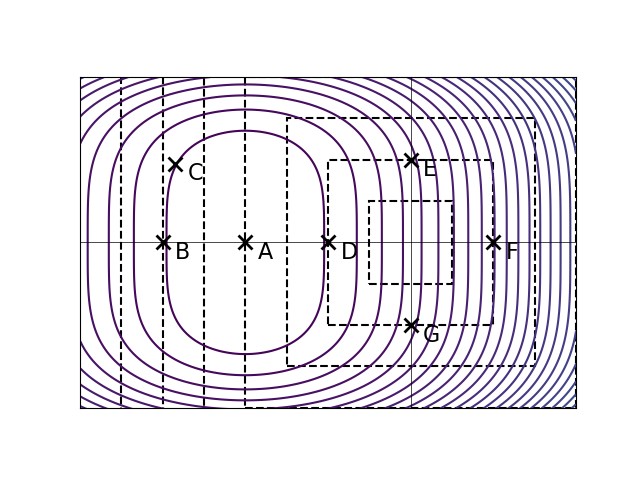
Let \(\tilde R(\vec w) = R(\vec w) + \lambda\|\vec w\|_\infty^2\), with \(\lambda > 0\). The point marked \(A\) is the minimizer of the unregularized risk. Suppose that it is known that one of the other points is the minimizer of the regularized risk, \(\tilde R(\vec w)\), for some unknown \(\lambda > 0\). Which point is it?
Solution
D.
Problem #086
Tags: regularization
Recall that in ridge regression, we solve the following optimization problem:
where \(\lambda > 0\) is a hyperparameter controlling the strength of regularization.
Suppose you solve the ridge regression problem with \(\lambda = 2\), and the resulting solution has a mean squared error of \(10\).
Now suppose you increase the regularization strength to \(\lambda = 4\) and solve the ridge regression problem again. True or False: it is possible that the mean squared error of the new solution is less than \(10\).
By ``mean squared error,'' we mean \(\frac1n \sum_{i=1}^n (y_i - \vec w \cdot\operatorname{Aug}(\nvec{x}{i}))^2\)
Solution
False.
Problem #091
Tags: regularization
The ``\(p = \frac12\)'' norm of a vector \(\vec w \in\mathbb R^d\), written \(\|\vec w\|_{\frac12}\), is defined as:
Let \(R(\vec w)\) be an unregularized risk function on a data set. The solid curves in the plot below are the contours of \(R(\vec w)\). The dashed lines show where \(\|\vec w\|_{\frac12}\) is equal to 1, 2, 3, and so on.
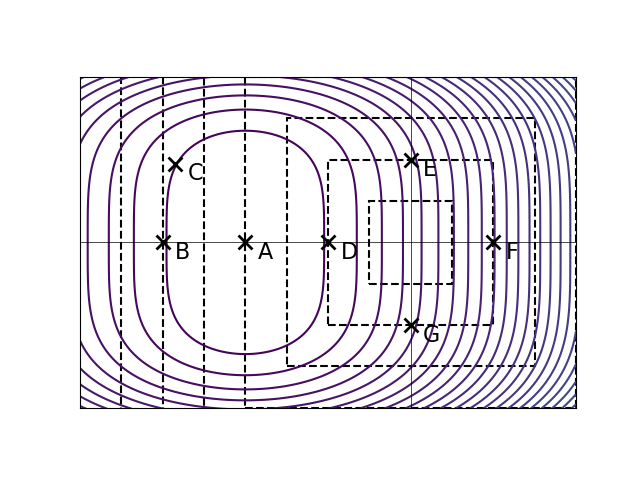
Let \(\tilde R(\vec w) = R(\vec w) + \lambda\|\vec w\|_{\frac12}\), with \(\lambda > 0\). The point marked \(A\) is the minimizer of the unregularized risk. Suppose it is known that one of the other points is the minimizer of the regularized risk, \(\tilde R(\vec w)\), for some unknown \(\lambda > 0\). Which point is it?
Solution
D.