Problems tagged with "conditional independence"

Problem #046

Tags: conditional independence

Recall that a deck of 52 cards contains:

Hearts: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A

Diamonds: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A

Clubs: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A

Spades: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A

Also recall that Hearts and Diamonds are red, while Clubs and Spades are black.

Part 1)

Suppose a single card is drawn at random.

Let \(A\) be the event that the card is a heart. Let \(B\) be the event that the card is a 5.

Are \(A\) and \(B\) independent events?

Solution

Yes, they are independent.

Part 2)

Suppose two cards are drawn at random (without replacing them into the deck).

Let \(A\) be the event that the second card is a heart. Let \(B\) be the event that the first card is red.

Are \(A\) and \(B\) independent events?

Solution

No, they are not.

Part 3)

Suppose two cards are drawn at random (without replacing them into the deck).

Let \(A\) be the event that the second card is a heart. Let \(B\) be the event that the second card is a diamond. Let \(C\) be the event that the first card is face card.

Are \(A\) and \(B\) conditionally independent given \(C\)?

Solution

No, they are not.

Problem #058

Tags: conditional independence

Suppose that a deck of cards has some cards missing. Namely, both the Ace of Spades and Ace of Clubs are missing, leaving 50 cards remaining.

Hearts: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A

Diamonds: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A

Clubs: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K

Spades: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K

Also recall that Hearts and Diamonds are red, while Clubs and Spades are black.

Part 1)

Suppose a single card is drawn at random.

Let \(A\) be the event that the card is a heart. Let \(B\) be the event that the card is an Ace.

Are \(A\) and \(B\) independent events?

Solution

No, they are not.

Part 2)

Suppose a single card is drawn at random.

Let \(A\) be the event that the card is a red. Let \(B\) be the event that the card is a heart. Let \(C\) be the event that the card is an ace.

Are \(A\) and \(B\) conditionally independent given \(C\)?

Solution

Yes, they are.

Part 3)

Suppose a single card is drawn at random.

Let \(A\) be the event that the card is a King. Let \(B\) be the event that the card is red. Let \(C\) be the event that the card is not a numbered card (that is, it is a J, Q, K, or A).

Are \(A\) and \(B\) conditionally independent given \(C\)?

Solution

No, they are not conditionally independent.

Problem #098

Tags: conditional independence

Suppose Justin has a dartboard at home that looks like the below:

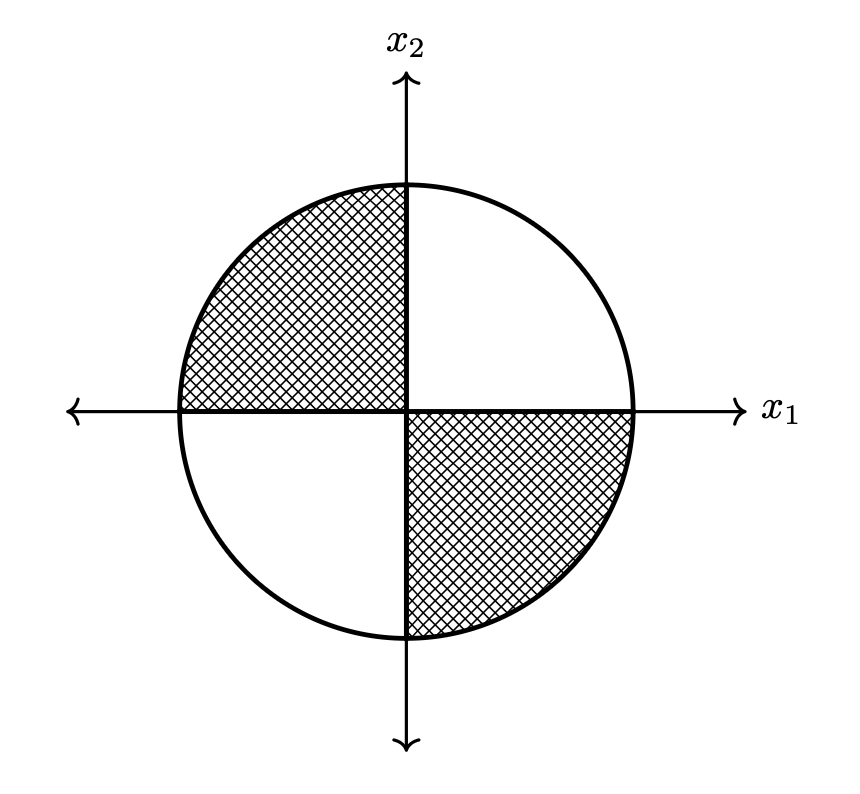
Justin uses the dartboard to determine how long the midterm will be: if he throws a dart and it lands in the shaded region, the midterm will have 17 questions; if it lands in the unshaded region, it will have 16 questions.

Assume that Justin's dart throws are drawn from a uniform distribution on the dartboard, and that the dart always hits the board (that is, the density function is constant everywhere on the dartboard, and zero off of the dartboard). Let \(X_1\) be the horizontal component of a dart throw and \(X_2\) be the vertical component. Let \(Q\) be the number of questions on the exam; since it is chosen randomly, it is also a random number.

Part 1)

True or False: \(X_1\) and \(X_2\) are independent.

True False
Solution

False.

Part 2)

True or False: \(X_1\) and \(X_2\) are conditionally independent given \(Q\).

True False
Solution

False.

Part 3)

True or False: \(X_1\) and \(Q\) are independent.

True False
Solution

True.

Part 4)

True or False: \(X_1\) and \(Q\) are conditionally independent given \(X_2\).

True False
Solution

False.

Solution

Video explanation: https://youtu.be/b4XlZsePCgU

Problem #114

Tags: conditional independence, Gaussians, covariance

Let \(X_1\) and \(X_2\) be two independent random variables. Suppose the distribution of \(X_1\) has the Gaussian density:

\[ p_1(x_1) = \frac{1}{\sqrt{8 \pi}}\, e^{-\frac{(x_1 - 2)^2}{8}}, \]

while the distribution of \(X_2\) has the Gaussian density:

\[ p_2(x_2) = \frac{1}{\sqrt{2\pi}}\, e^{-\frac{(x_2 + 1)^2}{2}}. \]

Which one of the following pictures shows the contours of the joint density \(p(x_1, x_2)\)(the density for the joint distribution of \(X_1\) and \(X_2\))?

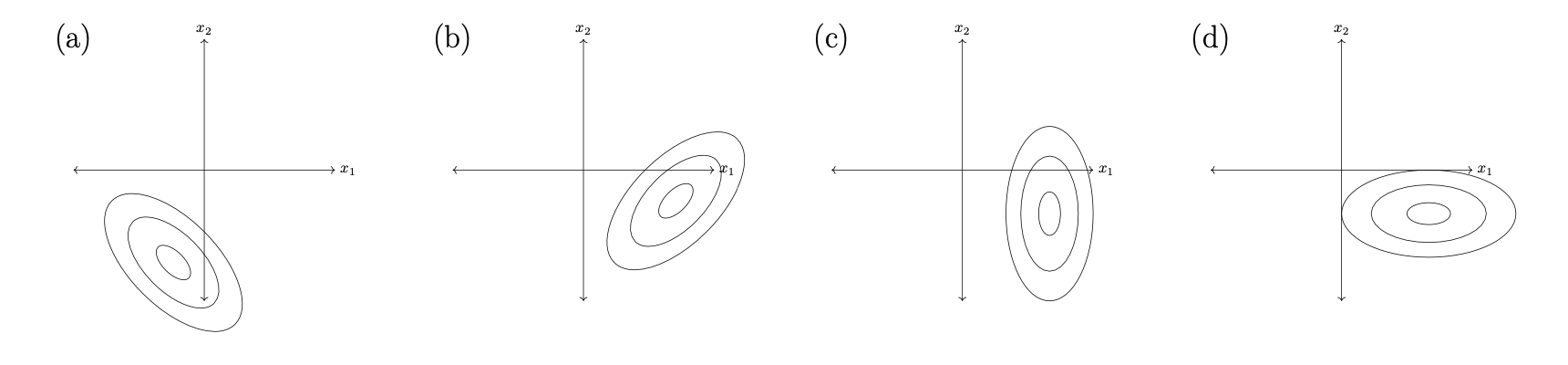
Solution

Picture (d).

Problem #122

Tags: conditional independence

Suppose that Justin has a wall at home that he has painted to look like the below:

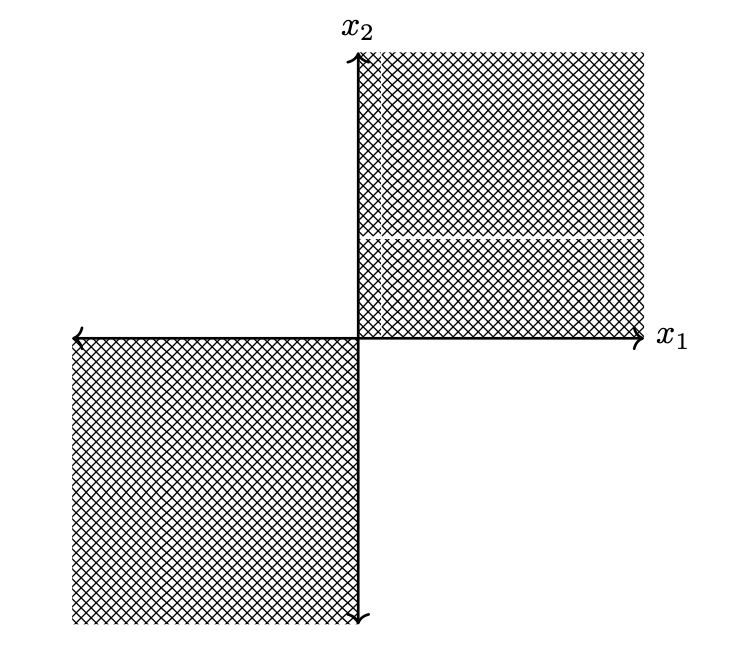
Justin uses the wall to determine how long Redemption Midterm 02 will be: if he throws a dart at the origin and it lands in the shaded region, the redemption midterm will have 14 questions; if it lands in the unshaded region, it will have 2 questions.

Assume that Justin's dart throws are drawn from a spherical Gaussian whose mean is at the origin. Let \(X_1\) be the horizontal component of a dart throw and \(X_2\) be the vertical component. Let \(Q\) be the number of questions on the exam; since it is chosen randomly, it is also a random number. You can assume that the wall is infinitely large, and that the shaded regions extend infinitely up and to the right, and down and to the left.

Part 1)

True or False: \(X_1\) and \(X_2\) are independent.

True False
Solution

True.

Part 2)

True or False: \(X_1\) and \(X_2\) are conditionally independent given \(Q\).

True False
Solution

False.

Part 3)

Let \(D = \sqrt{X_1^2 + X_2^2}\), and note that \(D\) is the distance of a dart throw from the origin. True or False: \(D\) and \(Q\) are independent.

True False
Solution

True.

Part 4)

True or False: \(X_1\) and and \(X_2\) are conditionally independent given \(D\).

True False
Solution

False.