Problems tagged with "subgradients"
Problem #008
Tags: subgradients
Consider the function \(f(x,y) = x^2 + |y|\). Plots of this function's surface and contours are shown below.
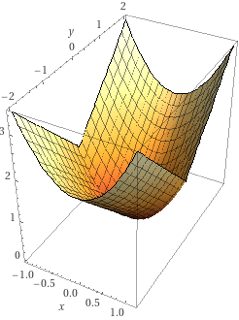
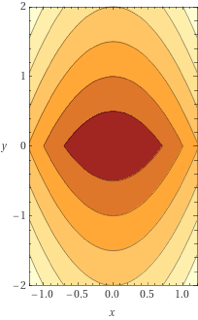
Which of the following are subgradients of \(f\) at the point \((0, 0)\)? Check all that apply.
Solution
\((0, 0)^T\), \((0, 1)^T\), and \((0, -1)^T\) are subgradients of \(f\) at \((0, 0)\).
Problem #025
Tags: subgradients
Consider the function \(f(x,y) = |x| + y^4\). Plots of this function's surface and contours are shown below.
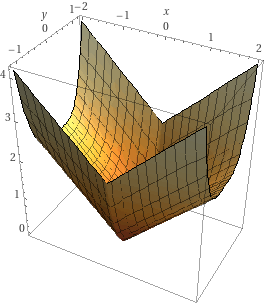
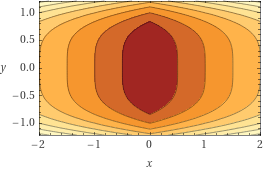
Write a valid subgradient of \(f\) at the point \((0, 1)\).
There are many possibilities, but you need only write one. For the simplicity of grading, please pick a subgradient whose coordinates are both integers, and write your answer in the form \((a, b)\), where \(a\) and \(b\) are numbers.
Solution
\((x, 4)\), where \(x \in[-1,1]\)
Problem #067
Tags: subgradients
Consider the piecewise function:
For convenience, a plot of this function is shown below:
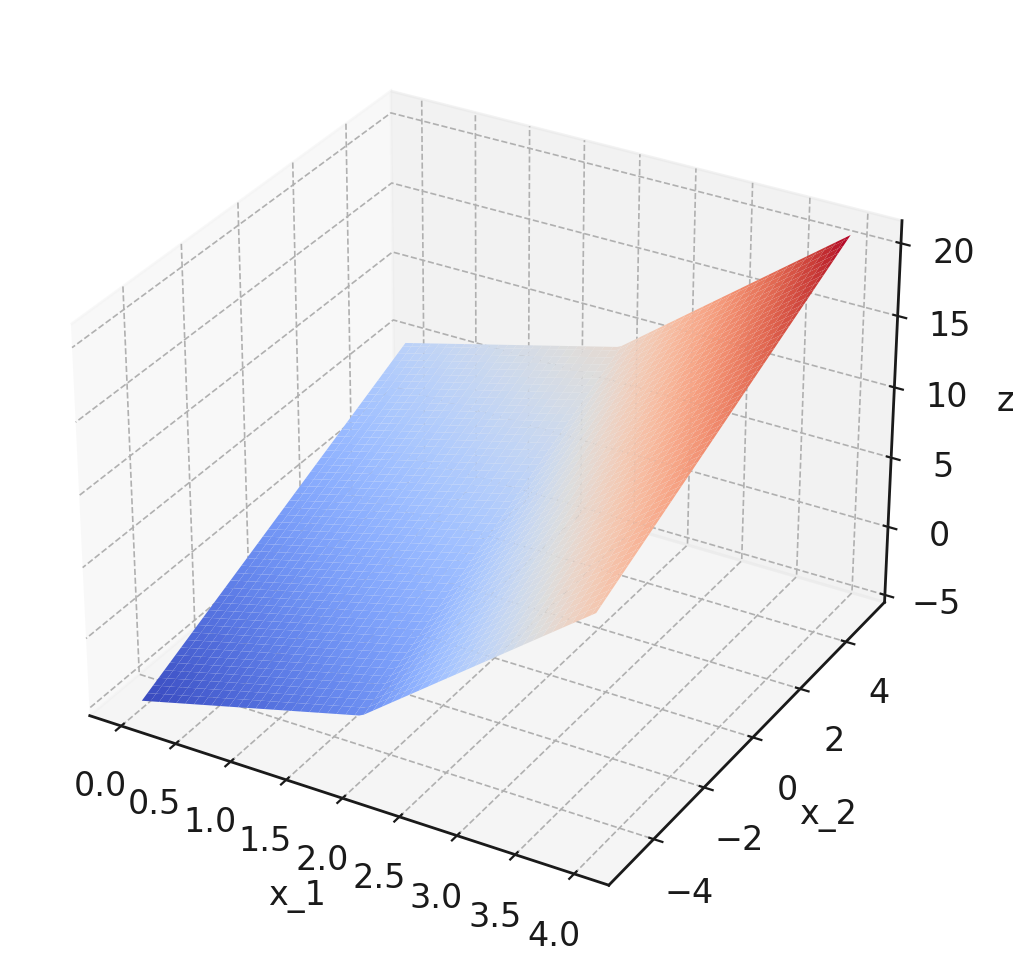
Note that the plot isn't intended to be precise enough to read off exact values, but it might help give you a sense of the function's behavior. In principle, you can do this question using only the piecewise definition of \(f\) given above.
Part 1)
What is the gradient of this function at the point \((0, 0)\)?
Part 2)
Which of the below are valid subgradients of the function at the point \((2,0)\)? Select all that apply.
Solution
\((3,1)^T\) and \((2,1)^T\) are valid subgradients of the function at \((2,0)\).
Problem #084
Tags: subgradients, gradients
Consider the following piecewise function that is linear in each quadrant:
For convenience, a plot of this function is shown below:
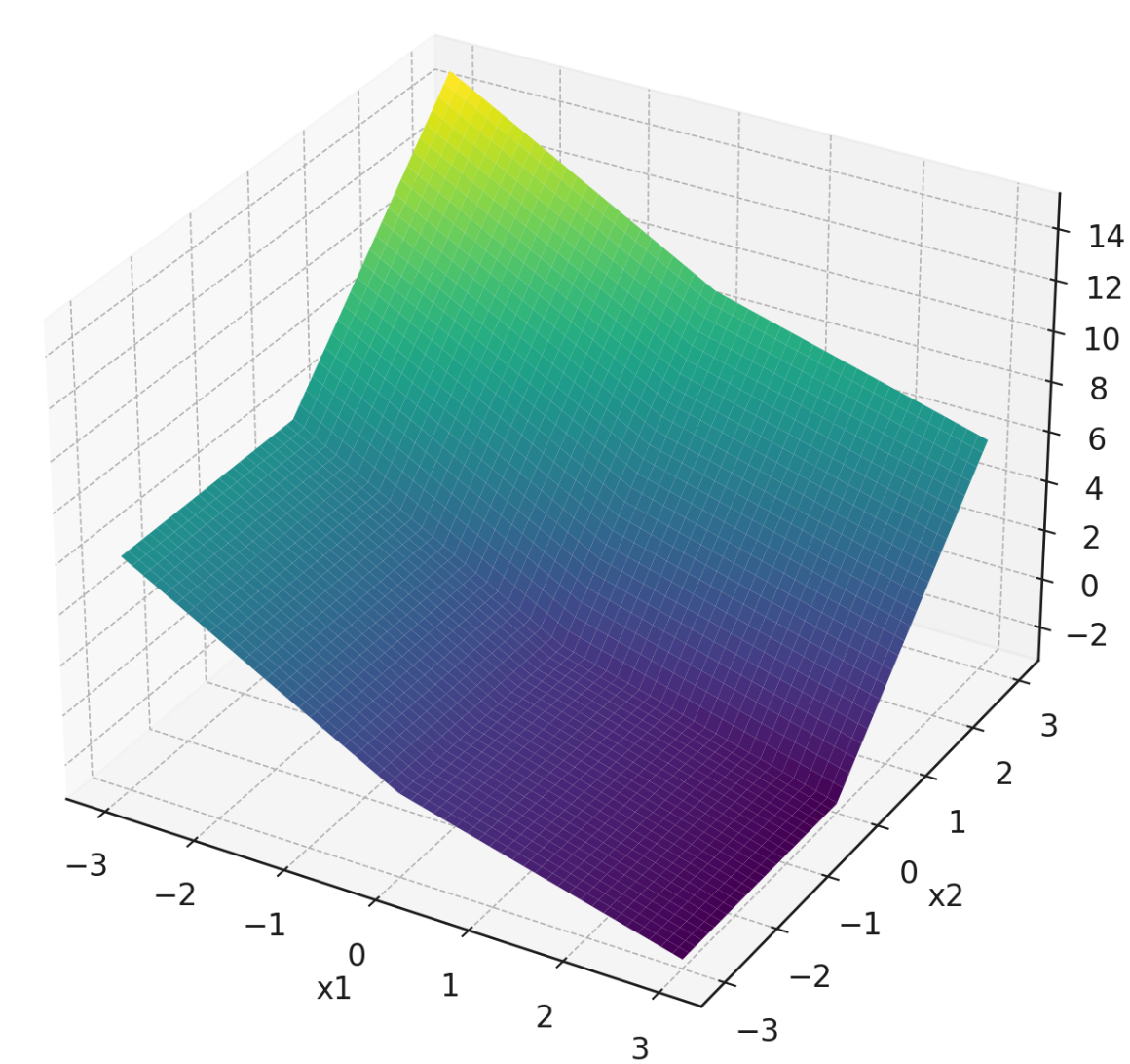
Note that the plot isn't intended to be precise enough to read off exact values, but it might help give you a sense of the function's behavior. In principle, you can do this question using only the piecewise definition of \(f\) given above.
Part 1)
What is the gradient of this function at the point \((1, 1)\)?
Part 2)
What is the gradient of this function at the point \((-1, -1)\)?
Part 3)
Which of the below are valid subgradients of the function at the point \((0,-2)\)? Select all that apply.
Solution
\((-2, 0)^T\) and \((-1.5, 0)^T\) are valid subgradients.
Part 4)
Which of the below are valid subgradients of the function at the point \((0,0)\)? Select all that apply.
Solution
\((-1, 3)^T\), \((-2, 0)^T\), and \((-1, 2)^T\) are valid subgradients.
Problem #085
Tags: gradient descent, subgradients
Recall that a subgradient of the absolute loss is:
Suppose you are running subgradient descent to minimize the risk with respect to the absolute loss in order to train a function \(H(x) = w_0 + w_1 x\) on the following data set:
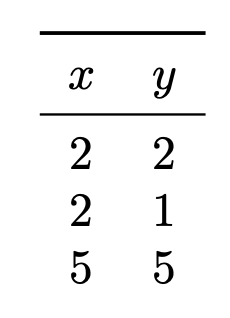
Suppose that the initial weight vector is \(\vec w = (0, 0)^T\) and that the learning rate is \(\eta = 1\). What will be the weight vector after one iteration of subgradient descent?