Problems tagged with "perceptrons"

Suppose gradient descent is to be used to train a perceptron classifier \(H(\vec x; \vec w)\) on a data set of \(n\) points, \(\{\nvec{x}{i}, y_i \}\). Recall that each iteration of gradient descent takes a step in the opposite direction of the ``gradient''.

Which gradient is being referred to here?

Suppose a perceptron classifier \(H(\vec x) = \vec w \cdot\vec x\) is trained on the data shown below. The points marked with ``+'' have label +1, while the ``\(\circ\)'' points have label -1. The perceptron's decision boundary is plotted as a thick solid line.

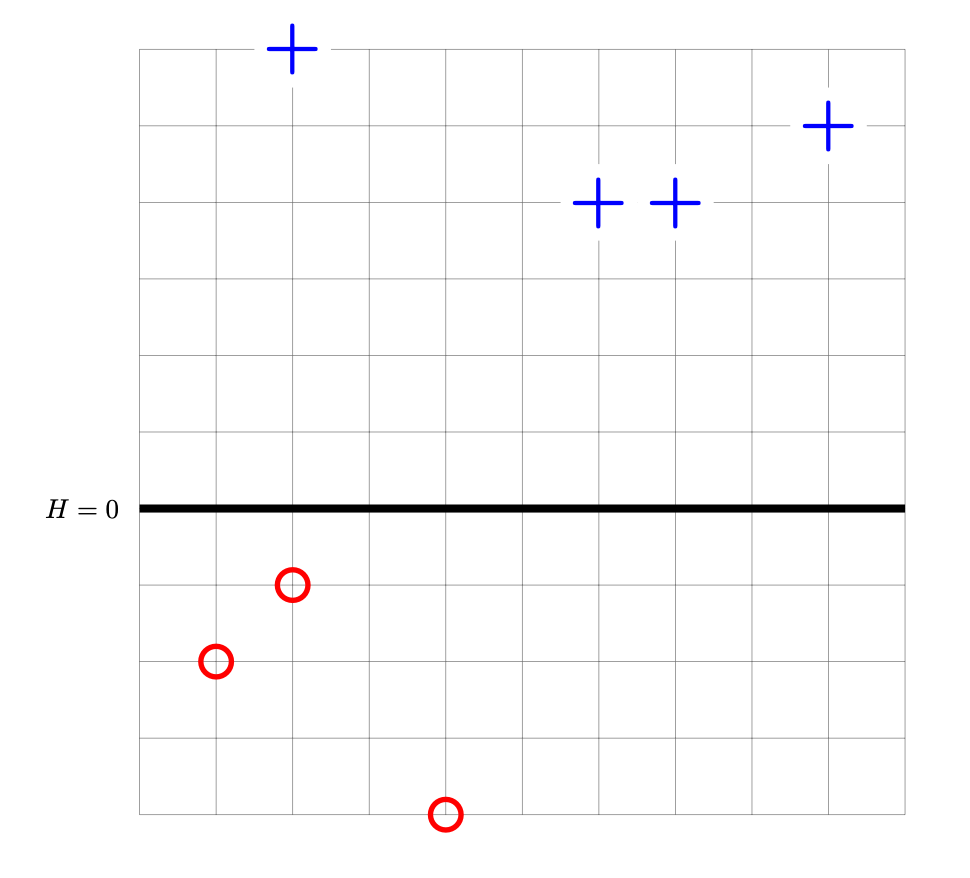
Let \(R(\vec w)\) be the risk with respect to the perceptron loss function, and let \(\vec w^*\) be the weight vector whose corresponding decision boundary is shown above.

True or False: the gradient of \(R\) evaluated at \(\vec w^*\) is \(\vec 0\).