Problems tagged with "linear and quadratic discriminant analysis"

Suppose a data set of points in \(\mathbb R^2\) consists of points from two classes: Class 1 and Class 0. The mean of the points in Class 1 is \((3,0)^T\), and the mean of points in Class 0 is \((7,0)^T\). Suppose Linear Discriminant Analysis is performed using the same covariance matrix \(C = \sigma^2 I\) for both classes, where \(\sigma\) is some constant.

Suppose there were 50 points in Class 1 and 100 points in Class 0.

Consider a new point, \((5, 0)^T\), exactly halfway between the class means. What will LDA predict its label to be?

Suppose the underlying class-conditional densities in a binary classification problem are known to be multivariate Gaussians.

Suppose a Quadratic Discriminant Analysis (QDA) classifier using full covariance matrices for each class is trained on a data set of \(n\) points sampled from these densities.

True or False: As the size of the data set grows (that is, as \(n \to\infty\)), the training error of the QDA classifier must approach zero.

Suppose Quadratic Discriminant Analysis (QDA) is used to train a classifier on the following data set of \((x_i, y_i)\) pairs, where \(x_i\) is the feature and \(y_i\) is the class label:

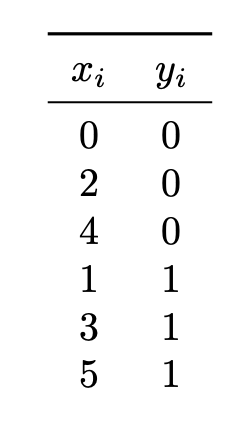
Univariate Gaussians are used to model the class conditional densities, each with their own mean and variance.

What is the prediction of the QDA classifier at \(x = 2.25\)?

The picture below shows the decision boundary of a binary classifier. The shaded region is where the classifier predicts for Class 1; everywhere else, the classifier predicts for Class 0.

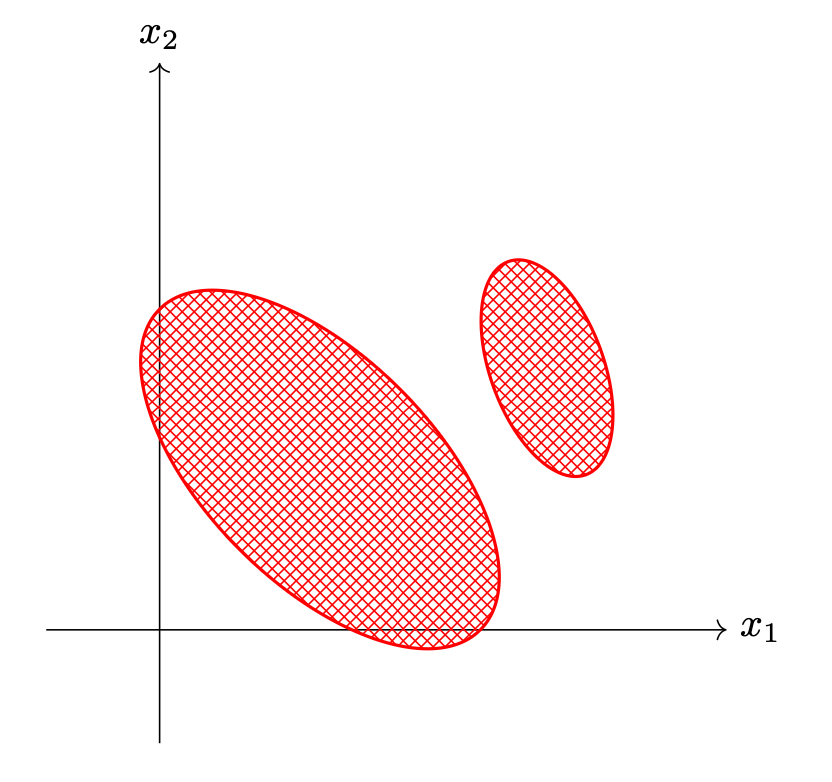
True or False: this could be the decision boundary of a Quadratic Discriminant Analysis (QDA) classifier that models the class-conditional densities as multivariate Gaussians with full covariance matrices.

The picture below shows the decision boundary of a binary classifier. The shaded region is where the classifier predicts for Class 1; everywhere else, the classifier predicts for Class 0. You can assume that the shaded region extends infinitely to the left and down.

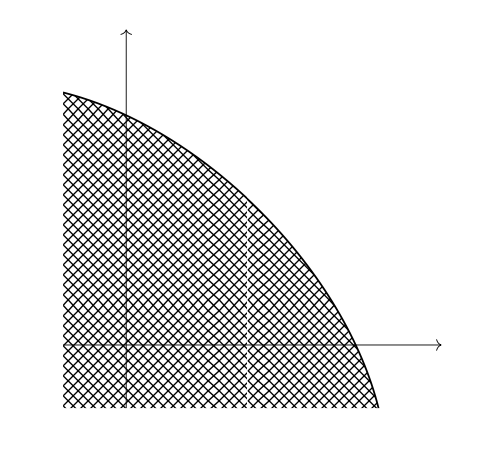
True or False: this could be the decision boundary of a classifier that estimates each class conditional density using two Gaussians with different means but the same, shared full covariance matrix, and applies the Bayes classification rule.