Problems tagged with "gradients"

Problem #009

Tags: gradient descent, perceptrons, gradients

Suppose gradient descent is to be used to train a perceptron classifier \(H(\vec x; \vec w)\) on a data set of \(n\) points, \(\{\nvec{x}{i}, y_i \}\). Recall that each iteration of gradient descent takes a step in the opposite direction of the ``gradient''.

Which gradient is being referred to here?

Solution

The gradient of the empirical risk with respect to \(\vec w\)

Problem #017

Tags: gradients

Let \(f(\vec w) = \vec a \cdot\vec w + \lambda\|\vec w \|^2\), where \(\vec w \in\mathbb R^d\), \(\vec a \in\mathbb R^d\), and \(\lambda > 0\).

What is the minimizer of \(f\)? State your answer in terms of \(\vec a\) and \(\lambda\).

Solution

\(\vec w^* = -\frac{\vec{a}}{2\lambda}\)

Problem #072

Tags: perceptrons, gradients

Suppose a perceptron classifier \(H(\vec x) = \vec w \cdot\vec x\) is trained on the data shown below. The points marked with ``+'' have label +1, while the ``\(\circ\)'' points have label -1. The perceptron's decision boundary is plotted as a thick solid line.

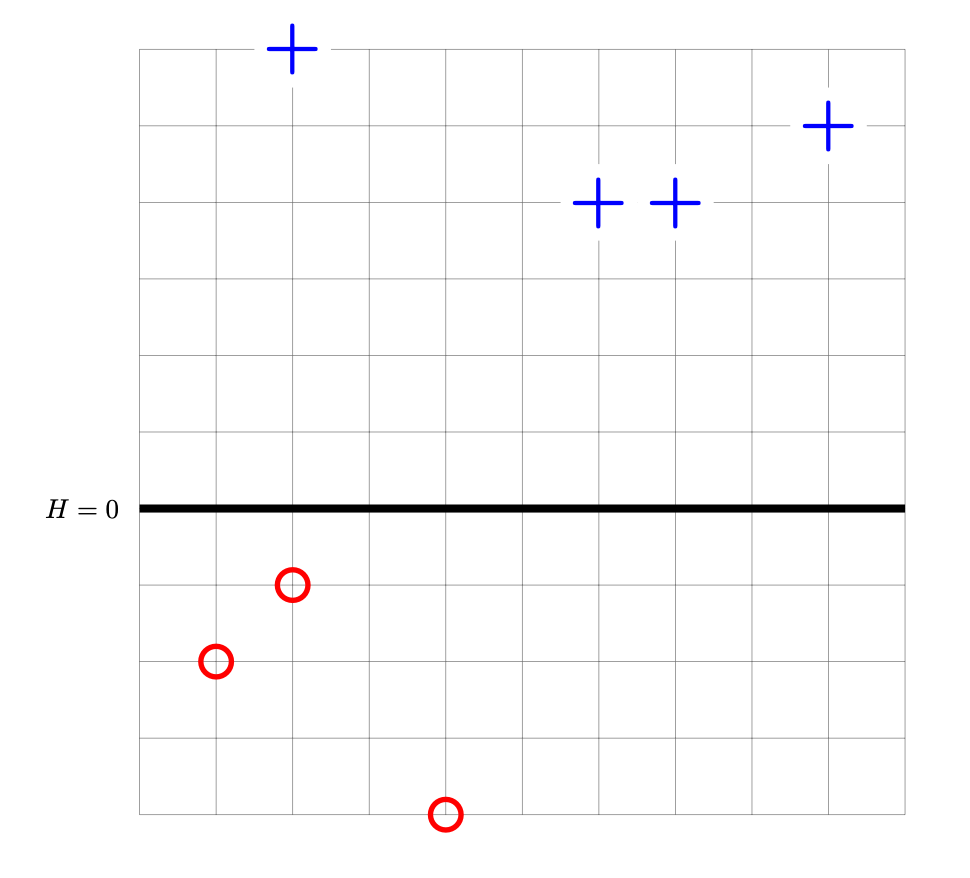
Let \(R(\vec w)\) be the risk with respect to the perceptron loss function, and let \(\vec w^*\) be the weight vector whose corresponding decision boundary is shown above.

True or False: the gradient of \(R\) evaluated at \(\vec w^*\) is \(\vec 0\).

True False
Solution

True.

Problem #074

Tags: gradients

Let \(\nvec{x}{1}, \ldots, \nvec{x}{n}\) be vectors in \(\mathbb R^d\) and let \(\vec w\) be a vector in \(\mathbb R^d\). Consider the function:

\[ f(\vec w) = \sum_{i=1}^n \vec w \cdot\nvec{x}{i} + \|\vec w \|^2, \]

What is \(\frac{d}{d \vec w} f(\vec w)\)?

Solution
\[\begin{align*} \frac{d}{d \vec w} \sum_{i=1}^n \vec w \cdot \nvec{x}{i} + \| \vec w \|^2 &= \frac{d}{d \vec w} \sum_{i=1}^n \vec w \cdot \nvec{x}{i} + \frac{d}{d \vec w} \| \vec w \|^2 \\ &= \sum_{i=1}^n \frac{d}{d \vec w} \vec w \cdot \nvec{x}{i} + \frac{d}{d \vec w} \| \vec w \|^2 \\ &= \sum_{i=1}^n \nvec{x}{i} + \frac{d}{d \vec w} \vec w^T \vec w \\ &= \sum_{i=1}^n \nvec{x}{i} + 2 \vec w \end{align*}\]

Problem #084

Tags: subgradients, gradients

Consider the following piecewise function that is linear in each quadrant:

\[ f(x_1, x_2) = \begin{cases} -2x_1, & \text{if } x_1 < 0 \text{ and } x_2 < 0,\\ % southwest -2x_1 + 3x_2, & \text{if } x_1 < 0 \text{ and } x_2 \geq 0,\\ % northwest -x_1 & \text{if } x_1 \geq 0 \text{ and } x_2 < 0,\\ % southeast -x_1 + 3x_2, & \text{if } x_1 \geq 0 \text{ and } x_2 \geq 0,\\ % northeast \end{cases}\]

For convenience, a plot of this function is shown below:

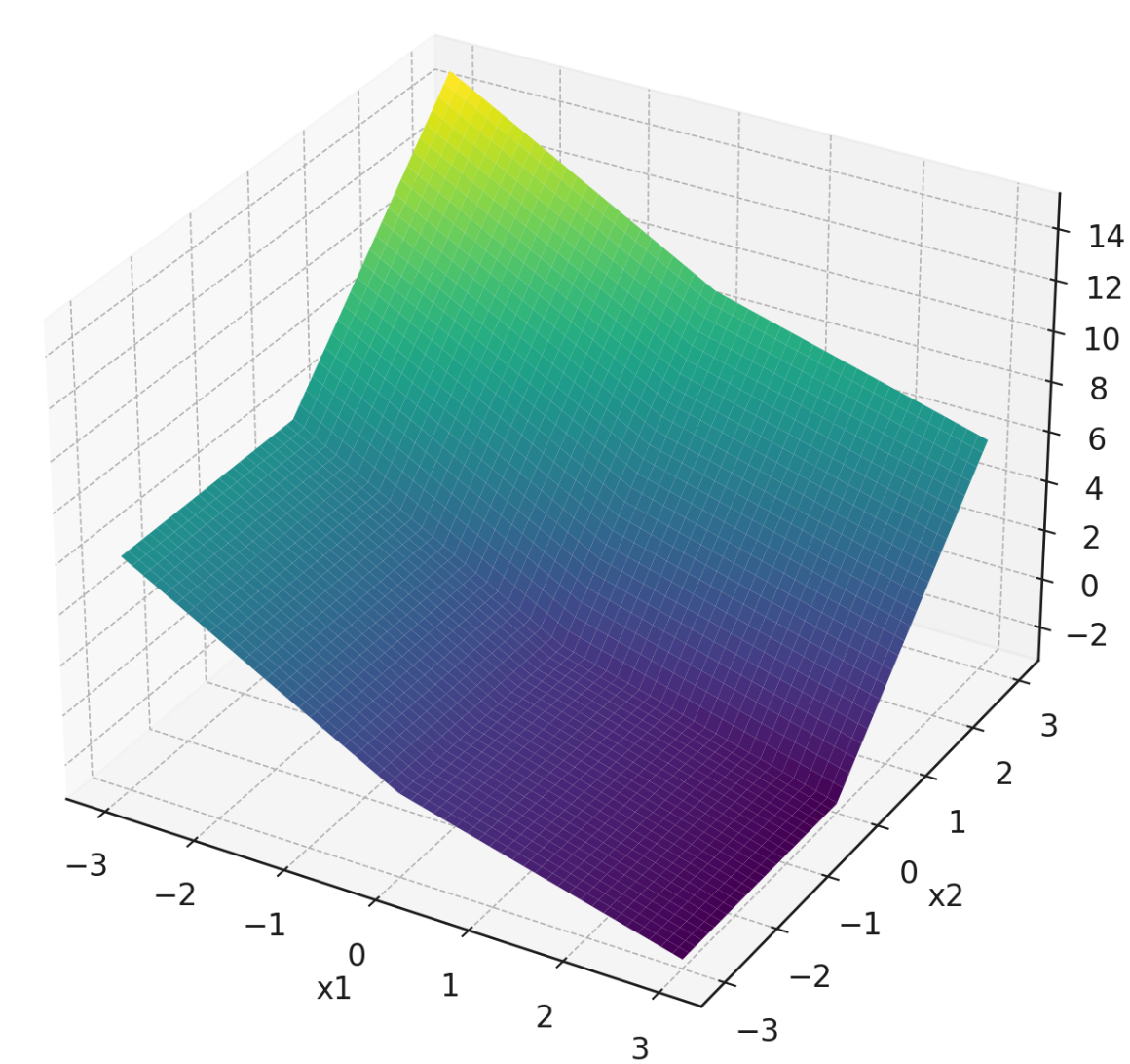
Note that the plot isn't intended to be precise enough to read off exact values, but it might help give you a sense of the function's behavior. In principle, you can do this question using only the piecewise definition of \(f\) given above.

Part 1)

What is the gradient of this function at the point \((1, 1)\)?

Part 2)

What is the gradient of this function at the point \((-1, -1)\)?

Part 3)

Which of the below are valid subgradients of the function at the point \((0,-2)\)? Select all that apply.

Solution

\((-2, 0)^T\) and \((-1.5, 0)^T\) are valid subgradients.

Part 4)

Which of the below are valid subgradients of the function at the point \((0,0)\)? Select all that apply.

Solution

\((-1, 3)^T\), \((-2, 0)^T\), and \((-1, 2)^T\) are valid subgradients.

Problem #089

Tags: SVMs, gradients

Consider the data set shown below. The points marked with ``+'' have label +1, while the ``\(\circ\)'' points have label -1. Shown are the places where a linear prediction function \(H\) is equal to zero (the thick solid line), 1, and -1 (the dotted lines). Each cell of the grid is 1 unit by 1 unit. The origin is not specified (it is not necssary to know the absolute coordinates of any points for this problem).

Let \(\vec w'\) be the parameter vector corresponding to prediction function \(H\) shown above. Let \(R(\vec w)\) be the risk with respect to the hinge loss on this data. True or False: the gradient of \(R\) evaluated at \(\vec w'\) is \(\vec 0\).

True False
Solution

True.

Problem #090

Tags: gradients

Let \(\vec x, \vec\mu,\) and \(\vec b\) be vectors in \(\mathbb R^n\), and let \(A\) be a symmetric \(n \times n\) matrix. Consider the function:

\[ f(\vec x) = \vec x^T A \vec x + (\vec x - \vec\mu) \cdot\vec b \]

What is \(\frac{d}{d \vec x} f(\vec x)\)?